Question

Дан куб АВСDА1В1С1D1 с ребром, равным 1. Найдите синус угла между плоскостями А1ВD и С1ВD

Answer 1

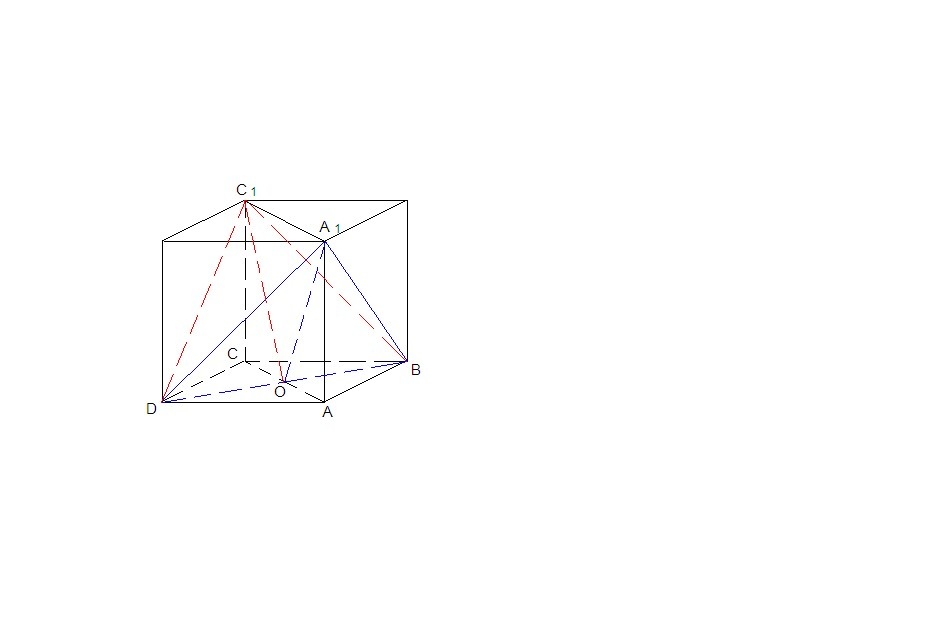
Пусть О - точка пересечения диагоналей нижнего основания.
Тогда СО⊥BD, CO - проекция С₁О на плоскость (АВС) ⇒ С₁О⊥BD по теореме о трех перпендикулярах.
Аналогично, А₁О⊥BD.
∠С₁ОА₁ - искомый. Обозначим его α.
ΔА₁BD = ΔС₁BD по трем сторонам (их стороны - диагонали равных квадратов)
Треугольники равносторонние со стороной √2.
А₁О = С₁О = √6/2 - как высота равностороннего треугольника.
ΔС₁ОА₁:
С₁А₁² = А₁О² + С₁О² - 2А₁О· С₁О·cosα
2 = 6/4 + 6/4 - 2 · √6/2 · √6/2 · cosα
2 = 3 - 3cosα
cosα = 1/3
α = arccos (1/3)