Предмет: Геометрия,
автор: a1400434
ВАЖЕН ЧЕРТЕЖ :з
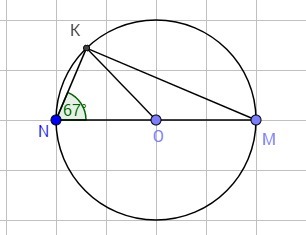
В окружности с центром O угол между диаметром MN и хордой NK равняется 67 градусов. Найдите углы KMN и MOK.
Ответы
Автор ответа:
4
В ΔKON:
ON = OK (радиусы), следовательно ΔКОN равнобедренный, с основанием КN.
В равнобедренном Δ углы при основании равны, следовательно
∠KOM = ∠KNM*2 = 2*67 = 134° (внешний угол Δ равен сумме внутренних углов, не смежных с данным углом).
В ΔКОМ:
КО = ОМ (радиусы), следовательно ΔКОМ равнобедренный, с основанием КМ.
В равнобедренном Δ углы при основании равны, следовательно:
∠KMN = (180 - 134):2 = 23°
Ответ: ∠KMN = 23°; ∠KOM = 134°.
ON = OK (радиусы), следовательно ΔКОN равнобедренный, с основанием КN.
В равнобедренном Δ углы при основании равны, следовательно
∠KOM = ∠KNM*2 = 2*67 = 134° (внешний угол Δ равен сумме внутренних углов, не смежных с данным углом).
В ΔКОМ:
КО = ОМ (радиусы), следовательно ΔКОМ равнобедренный, с основанием КМ.
В равнобедренном Δ углы при основании равны, следовательно:
∠KMN = (180 - 134):2 = 23°
Ответ: ∠KMN = 23°; ∠KOM = 134°.
Приложения:
a1400434:
Спасибо <З
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Английский язык,
автор: VAPROLINA20
Предмет: Геометрия,
автор: ryzenkovivan4
Предмет: Алгебра,
автор: machkasovanatalya
Предмет: Математика,
автор: ThePutika