Предмет: Алгебра,
автор: Володя203
Докажите что треугольник с вершинами в серединах сторон равнобедренного треугольника является равнобедренным.
Ответы
Автор ответа:
0
Пусть АВС - равнобедренный треугольник, АВ=ВС,
Е -середина АB, К -середина ВС, Т - середина АС
Нужно доказать, что ЕКТ - треугольник, с вершинами в серединах сторон треугольника является равнобедренным
Тогда ЕК, ЕТ, КТ - среднии линии треугольника АВС,
по свойству средних линий (средняя линия треугольника равна половине соответствующей стороны)
EK=AC/2; KT=AB/2; ET=BC/2
откуда получаем, что
KT=AB/2=BC/2=ET
по определению треугольник ЕКТ равнобедренный (так как у него есть две равные стороны)
Доказано.
Е -середина АB, К -середина ВС, Т - середина АС
Нужно доказать, что ЕКТ - треугольник, с вершинами в серединах сторон треугольника является равнобедренным
Тогда ЕК, ЕТ, КТ - среднии линии треугольника АВС,
по свойству средних линий (средняя линия треугольника равна половине соответствующей стороны)
EK=AC/2; KT=AB/2; ET=BC/2
откуда получаем, что
KT=AB/2=BC/2=ET
по определению треугольник ЕКТ равнобедренный (так как у него есть две равные стороны)
Доказано.
Приложения:
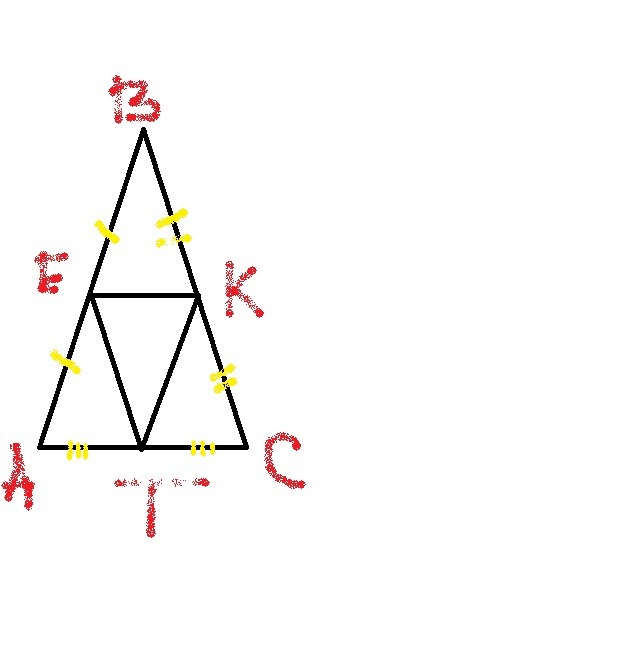
Похожие вопросы
Предмет: Алгебра,
автор: vitkaapipo
Предмет: Химия,
автор: aroslavpetrik1p41q7i
Предмет: Литература,
автор: MAXCHE05
Предмет: Физика,
автор: малая1703
Предмет: Математика,
автор: goldenbel