Предмет: Алгебра,
автор: DI3
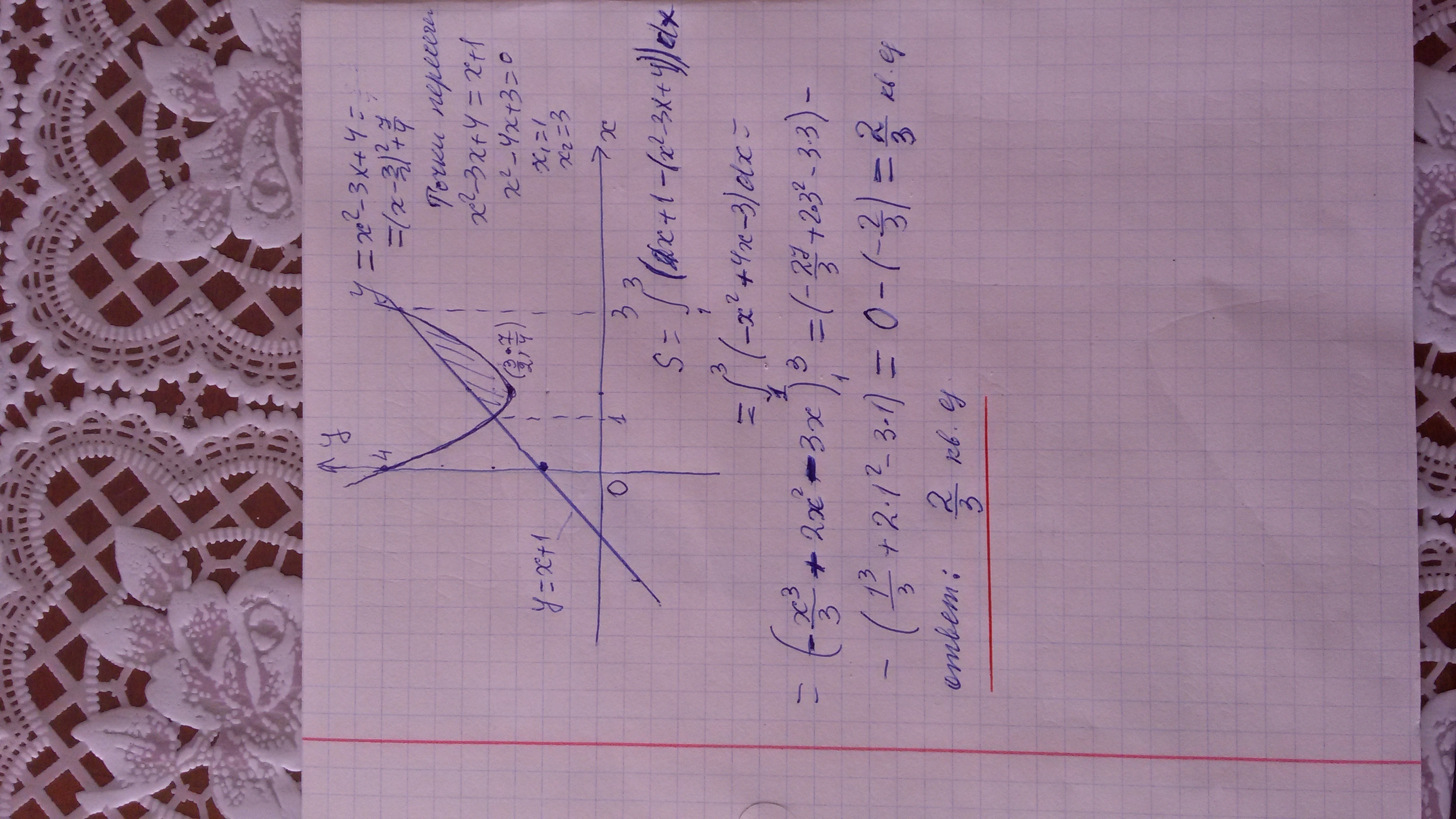
Найти площадь фигуры: y=x^2-3x+4, y=x+1
Ответы
Автор ответа:
0
task/24693872
---.---.---.---.---.---.
Найти площадь фигуры: y=x²-3x+4, y=x+1
y = x²-3x+4 =(x -3/2)² +7/4 , B(3/2 ; 7/4) _ вершина параболы
точки пересечения графиков функции
y=x²-3x+4, и y=x+1
x²-3x+4 =x+1 ;
x²-4x+3 =0 ; * * * x²-4x+3 = x²-x -3x+3 =x(x-1) -3(x-1)=(x-1)(x-3) * * *
D/4 = 2² -3=1 * * *коэффициент переменной x равен(-4)_четное число * * *
x₁=2 -1 =1 ;
x₂ =2+1 =3
S = ∫³ (x+1 -(x²-3x+4) dx = ∫³ ( -x²+4x-3) dx = ...
₁ ₁
см приложения
---.---.---.---.---.---.
Найти площадь фигуры: y=x²-3x+4, y=x+1
y = x²-3x+4 =(x -3/2)² +7/4 , B(3/2 ; 7/4) _ вершина параболы
точки пересечения графиков функции
y=x²-3x+4, и y=x+1
x²-3x+4 =x+1 ;
x²-4x+3 =0 ; * * * x²-4x+3 = x²-x -3x+3 =x(x-1) -3(x-1)=(x-1)(x-3) * * *
D/4 = 2² -3=1 * * *коэффициент переменной x равен(-4)_четное число * * *
x₁=2 -1 =1 ;
x₂ =2+1 =3
S = ∫³ (x+1 -(x²-3x+4) dx = ∫³ ( -x²+4x-3) dx = ...
₁ ₁
см приложения
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: busabibi
Предмет: Английский язык,
автор: Maryal666
Предмет: Математика,
автор: ivanschenko
Предмет: Математика,
автор: АнгелДевочка