помогите пожалуйста
геометрия 7 класс

Ответы
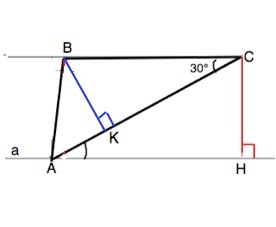
В треугольнике АВС угол С=30°, АС=10 см, ВС=8 см. Через вершину А проведена прямая а, параллельная ВС. Найдите:
а) расстояние от точки В до прямой АС;
б) расстояние между прямыми а и ВС.
а) Расстояние от точки до прямой ― это длина перпендикуляра, опущенного из данной точки на данную прямую.
Опустим из В перпендикуляр ВК на АС. Треугольник ВКС - прямоугольный, ВК - катет, противолежит углу 30°, следовательно, равен половине гипотенузы ВС (свойство). ВК=8:2=4 см.
б) Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой.
Опустим из т. С перпендикуляр на прямую а и пересекающий её в точке Н.
∆ АНС - прямоугольный по построению, угол САН=С=30° как накрестлежащие при пересечении параллельных прямых а и ВС, АС – гипотенуза ∆ АСН.
Катет СН противолежит углу 30° и по свойству такого катета равен половине гипотенузы АС.
СН=10:2=5 см. - это расстояние между прямыми ВС и а.