Предмет: Геометрия,
автор: kirill0501
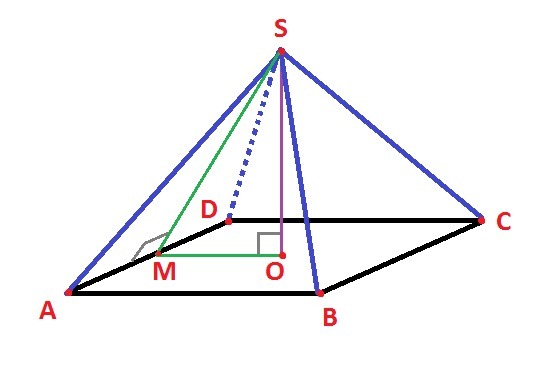
В правильной четырехугольной пирамиде сторона основания равна 4 м, а высота 2 м. Найти угол наклона боковой грани к плоскости основания, площадь полной поверхности пирамиды.
Ответы
Автор ответа:
0
∠SMO = ∠MSO, также ∠MOS = 90°, тогда ∠SMO =
S(п.пов) = S(бок.бов) + S(осн).
S(бок.бов) =
S(осн.) = 4 * 4 = 16.
S(п.пов)
Приложения:
Похожие вопросы
Предмет: Физика,
автор: antipovtheme
Предмет: Математика,
автор: miranur
Предмет: Английский язык,
автор: olenkadmitrik
Предмет: География,
автор: dropdrap1
Предмет: Математика,
автор: aevstifeeva22