Предмет: Геометрия,
автор: peperoni815
Апофема правильной шестиугольной пирамиды равна 10 см,а угол между боковой гранью и основанием равен 45 градусов.Найдите площадь боковой поверхности пирамиды.
Помогите кто нибудь))
Ответы
Автор ответа:
0
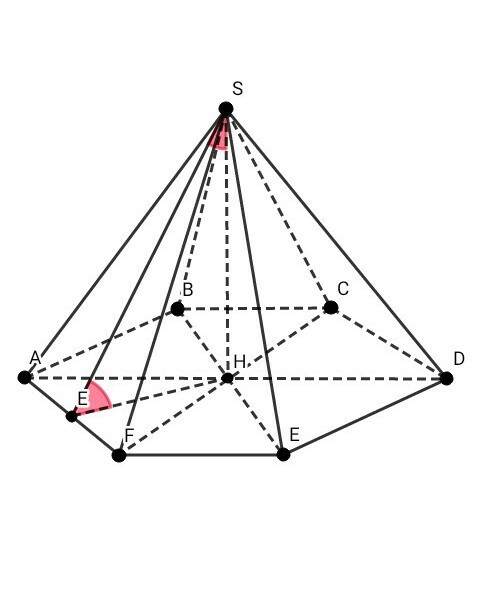
ДАНО: SABCDEF - правильная шестиугольная пирамида ; SE = 10 см ; угол между боковой гранью SAF и основанием ABCDEF ( FAH ) равен 45°
НАЙТИ: S бок. пов.
______________________________
1) угол между боковой гранью SAF и основанием ABCDEF ( FAH ) — это линейный угол двугранного угла HFAS.
Линейным углом двугранного угла называется угол, образованный лучами с вершиной на ребре, лучи которого лежат на гранях двугранного угла и перпендикулярны ребру
2) Рассмотрим ∆ SAF ( SA = SF ):
Опустили высоту SE
Высота в равнобедренном треугольнике является и медианой, и биссектрисой → AE = EF
отрезок SH ( высота пирамиды ) перпендикулярен ( АВС )
Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости
Значит, SH перпендикулярен НЕ
SE перпендикулярен AF
Из этого следует, что НЕ перпендикулярен АF по теореме о трёх перпендикулярах
Соответственно, угол SEH = 45° - линейный угол двугранного угла HFAS
2) Рассмотрим ∆ SEH (угол SHE = 90°):
Сумма острых углов в прямоугольном треугольнике всегда равна 90° →
угол ESH = 90° - 45° = 45°
Значит, ∆ SEH — прямоугольный и равнобедренный, SH = EH
По теореме Пифагора:
ES² = SH² + EH²
ES² = 2 × SH²
10² = 2 × SH²
SH² = 100/2 = 50
SH = EH = 5√2 см
3) В основании правильной шестиугольной пирамиды лежит правильный шестиугольник. Бо'льшие диагонали прав. шестиугольника пересекаются в одной точке и делятся пополам, к тому же бо'льшие диагонали являются биссектрисами шестиугольника. Все углы прав. шестиугольника равны 120°.
Рассмотрим ∆ FAH :
угол HAF = угол AFH = 60°
Соответственно, угол AHF = 180° - 60° - 60° = 60°
Значит, ∆ FAH — равносторонний
AF = AH = HF
Сторона равностороннего треугольника вычисляется по формуле:

где а - сторона равностороннего треугольник, h - высота →
AF = ( 2√3 × HE ) / 3 = 2√3 × 5√2 / 3 = 10√6 / 3 см
4) У правильной шестиугольной пирамиды всего шесть боковых граней и все они равны друг другу →
S бок. пов. = 6 × S saf = 6 × ( 1/2 ) × 10 × ( 10√6 / 3 ) =

ОТВЕТ: S бок. пов. = 100√6 см²
НАЙТИ: S бок. пов.
______________________________
1) угол между боковой гранью SAF и основанием ABCDEF ( FAH ) — это линейный угол двугранного угла HFAS.
Линейным углом двугранного угла называется угол, образованный лучами с вершиной на ребре, лучи которого лежат на гранях двугранного угла и перпендикулярны ребру
2) Рассмотрим ∆ SAF ( SA = SF ):
Опустили высоту SE
Высота в равнобедренном треугольнике является и медианой, и биссектрисой → AE = EF
отрезок SH ( высота пирамиды ) перпендикулярен ( АВС )
Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости
Значит, SH перпендикулярен НЕ
SE перпендикулярен AF
Из этого следует, что НЕ перпендикулярен АF по теореме о трёх перпендикулярах
Соответственно, угол SEH = 45° - линейный угол двугранного угла HFAS
2) Рассмотрим ∆ SEH (угол SHE = 90°):
Сумма острых углов в прямоугольном треугольнике всегда равна 90° →
угол ESH = 90° - 45° = 45°
Значит, ∆ SEH — прямоугольный и равнобедренный, SH = EH
По теореме Пифагора:
ES² = SH² + EH²
ES² = 2 × SH²
10² = 2 × SH²
SH² = 100/2 = 50
SH = EH = 5√2 см
3) В основании правильной шестиугольной пирамиды лежит правильный шестиугольник. Бо'льшие диагонали прав. шестиугольника пересекаются в одной точке и делятся пополам, к тому же бо'льшие диагонали являются биссектрисами шестиугольника. Все углы прав. шестиугольника равны 120°.
Рассмотрим ∆ FAH :
угол HAF = угол AFH = 60°
Соответственно, угол AHF = 180° - 60° - 60° = 60°
Значит, ∆ FAH — равносторонний
AF = AH = HF
Сторона равностороннего треугольника вычисляется по формуле:
где а - сторона равностороннего треугольник, h - высота →
AF = ( 2√3 × HE ) / 3 = 2√3 × 5√2 / 3 = 10√6 / 3 см
4) У правильной шестиугольной пирамиды всего шесть боковых граней и все они равны друг другу →
S бок. пов. = 6 × S saf = 6 × ( 1/2 ) × 10 × ( 10√6 / 3 ) =
ОТВЕТ: S бок. пов. = 100√6 см²
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: xXataiXx
Предмет: Английский язык,
автор: alenakoz5
Предмет: География,
автор: kamillanuridin
Предмет: Математика,
автор: Аноним