Question

в основу правильної трикутної піраміди вписане коло радіусом 3 корінь з 3 см.знайти площу бічної поверхні піраміди якщо її апофема дорівнює 9см

Answer 1

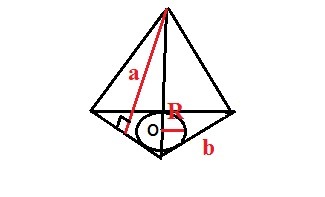
В основании правильной треугольной пирамиды лежит правильный (равносторонний) треугольник.
Радиус окружности, вписанной в правильный треугольник:
         b
r = ----------- , где b - сторона правильного треугольника
        2√3

b = r * 2√3 
b = 3√3 * 2√3 = 6 * 3 = 18 (cм)

Периметр треугольника - сумма длин всех сторон
p = b + b + b = 3b
p = 3 * 18 = 54 (cм)

Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на апофему:
S= 1/2 * p * a, где p - периметр основания пирамиды, а - апофема

S = 1/2 * 54 * 9 = 243 (cм²)