Предмет: Алгебра,
автор: ashixminas
Помогите пожалуйста решить тригонометрические уравнения!!!!!! Заранее спасибо!!!!!
Приложения:
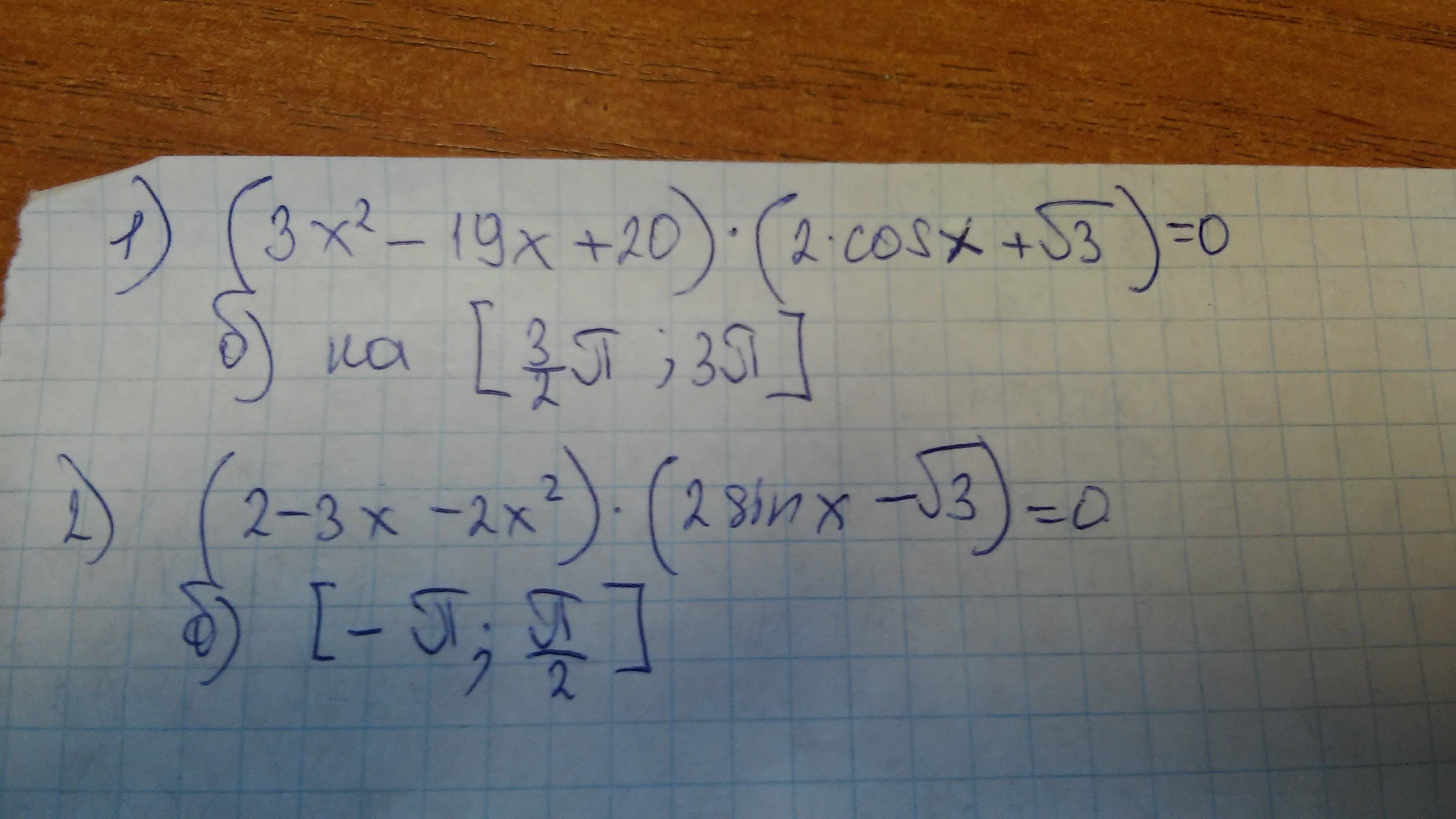
Ответы
Автор ответа:
0
1.  , ответ:
, ответ: 
1,1)

1,2)

на![[frac{3pi}{2};3pi] [frac{3pi}{2};3pi]](https://tex.z-dn.net/?f=%5Bfrac%7B3pi%7D%7B2%7D%3B3pi%5D) лежит только 1 корень, и он равен
лежит только 1 корень, и он равен 
2. , ответ:
, ответ: 
2,1)

2,2)

на![[-pi;frac{pi}{2}] [-pi;frac{pi}{2}]](https://tex.z-dn.net/?f=%5B-pi%3Bfrac%7Bpi%7D%7B2%7D%5D) лежат 2 корня, и они равны
лежат 2 корня, и они равны 
1,1)
1,2)
на
2.
2,1)
2,2)
на
Похожие вопросы
Предмет: Биология,
автор: valentinabilbas54
Предмет: Алгебра,
автор: zagorskiy07
Предмет: Литература,
автор: liaisan200877
Предмет: Биология,
автор: кэтлин1
Предмет: Математика,
автор: Драгнилия