Question

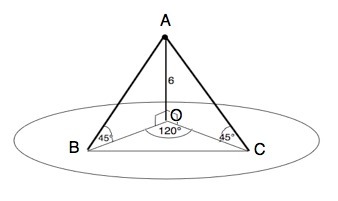
Из точки,удаленной от плоскости 6 см,проведены две наклонные.Найдите расстояние между основаниями наклонных,если угол между их проекциями равен 120 градусов,а каждая наклонная образует с плоскостью угол 45 градусов.С Рисунком пожалуйста.

Answer 1

 Расстояние от точки до плоскости  равно длине отрезка, опущенного из точки к плоскости перпендикулярно. 

Обозначим наклонные АВ и АС 

АО -  расстояние  от А до плоскости, перпендикулярно ей  и равно 6

 Углы АВО=АСО= 45°,  следовательно, треугольники АОВ и АОС равнобедренные и равны, ⇒ проекции наклонных  

ВО=СО=6 см. 

Соединив В и С, получим равнобедренный треугольник ВОС. 

Угол ВОС=120°, след. углы ОВС=ОСВ=30°. 

По т.синусов 

$frac{BC}{sin 120^{o}} = frac{OB}{sin 30^{o} }$

$BC: frac{ sqrt{3} }{2} =OB: frac{1}{2}$

2BC:√3=2•OB

BC=OB√3=6√3