Предмет: Алгебра,
автор: Изоабэлла
Решить неравенство
(неравенство на картинке)
Приложения:
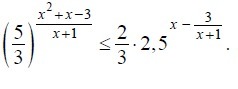
Ответы
Автор ответа:
0
Решить неравенство (5/3)^ (x²+x-3) / (x+1) ≤ (2/3)*2,5^(x -3/(x+1)) ;
---.---.---.---.---. ---.---.---.---.---. ---.---.---.---.---. ---.---.---.---.---. ---.---.---.
(5/3)^ (x²+x-3) /(x+1) ≤ (2/3)*2,5^(x -3/(x+1)) ;
* * *2,5 =5/2 и x -3/(x+1) = (x(x+1) -3 ) /(x+1)=(x² +x -3 ) /(x+1) * * *
(5/3)^ (x²+x-3) /(x+1) ≤ (2/3)*(5/2) ^(x²+x-3)/ (x+1) || умнож.(2/5) ^(x²+x-3)/ (x+1)
((5/3) * (2/5))^ (x²+x-3) /(x+1) ≤ (2/3) ;
(2/3) ^ (x²+x-3) /(x+1) ≤ (2/3) ; * * * 0 < 2/3 <1* * *
(x²+x-3) /(x+1) ≥1 ;
(x²+x-3) /(x+1) -1 ≥ 0 ;
(x²+x-3- x -1) /(x+1) ≥ 0 ;
(x² -4) /(x+1) ≥ 0 ;
(x+2)(x-2) /(x+1) ≥ 0 ;
методом интервалов
" -" "+" " -" "+"
-------------- [- 2] ////////////// (-1) ----------[2 ]////////////////////
ответ : x ∈ [ -2; -1) ∪ [2 ; ∞) .
* * * * * * * * * * * * * * * * * * * * * *
лучшее на бумаге → Решение в прикрепленном файле
---.---.---.---.---. ---.---.---.---.---. ---.---.---.---.---. ---.---.---.---.---. ---.---.---.
(5/3)^ (x²+x-3) /(x+1) ≤ (2/3)*2,5^(x -3/(x+1)) ;
* * *2,5 =5/2 и x -3/(x+1) = (x(x+1) -3 ) /(x+1)=(x² +x -3 ) /(x+1) * * *
(5/3)^ (x²+x-3) /(x+1) ≤ (2/3)*(5/2) ^(x²+x-3)/ (x+1) || умнож.(2/5) ^(x²+x-3)/ (x+1)
((5/3) * (2/5))^ (x²+x-3) /(x+1) ≤ (2/3) ;
(2/3) ^ (x²+x-3) /(x+1) ≤ (2/3) ; * * * 0 < 2/3 <1* * *
(x²+x-3) /(x+1) ≥1 ;
(x²+x-3) /(x+1) -1 ≥ 0 ;
(x²+x-3- x -1) /(x+1) ≥ 0 ;
(x² -4) /(x+1) ≥ 0 ;
(x+2)(x-2) /(x+1) ≥ 0 ;
методом интервалов
" -" "+" " -" "+"
-------------- [- 2] ////////////// (-1) ----------[2 ]////////////////////
ответ : x ∈ [ -2; -1) ∪ [2 ; ∞) .
* * * * * * * * * * * * * * * * * * * * * *
лучшее на бумаге → Решение в прикрепленном файле
Приложения:

Похожие вопросы
Предмет: Биология,
автор: godKape
Предмет: Геометрия,
автор: uucenik141
Предмет: Математика,
автор: aminainkz
Предмет: Физика,
автор: cjr55djlf
Предмет: Математика,
автор: Аноним