Предмет: Алгебра,
автор: Кариночка78
Помогите, пожалуйста, решить. Подробно. Срочно.
Приложения:
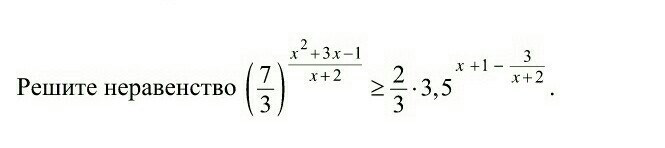
Ответы
Автор ответа:
0
так как
перепишем неравенство в виде
с учетом что
разделим обе части неравенства на
без смены знака неравенства
при этом используя свойство
получим
так как основание
то неравенство равносильно неравенству
далее метод интервалов
(критические точки разбивают числовую прямую на промежутку сохраняющие знак - все значения на промежутке либо положительны, либо отрицательные)
критические точки x+3=0; x=-3 - точка нечетной степени (при переходе через нее знак поменяется), обязательно входит в множество решений
x-1=0;x=1- точка нечетной степени (при переходе через нее знак поменяется), обязательно входит в множество решений
x+2=0; x=-2 - точка нечетной степени (при переходе через нее знак поменяется), НЕ входит в множество решений (так как в знаменателе)
при х=100000 >1 левая часть очевидно со знаком +
итого получаем разбивку
(знак -)[-3] (знак+) (-2) {знак -}[1] (знак +)
<=0 - соответствует промежуткам со знаком -
получаем ответ
Приложения:


Похожие вопросы