Question

В прямоугольном треугольнике точка соприкосновения вписанной окружности делит катет на отрезки 3 см и 5 см. Найти площадь треугольника.
____________________________________________________
У прямокутному трикутнику точка дотику вписаного кола ділить катет на відрізки 3 см і 5 см. Знайти площу трикутника.

Напишите пожалуйста не только ответ, но и решение. Заранее спасибо.

Answer 1

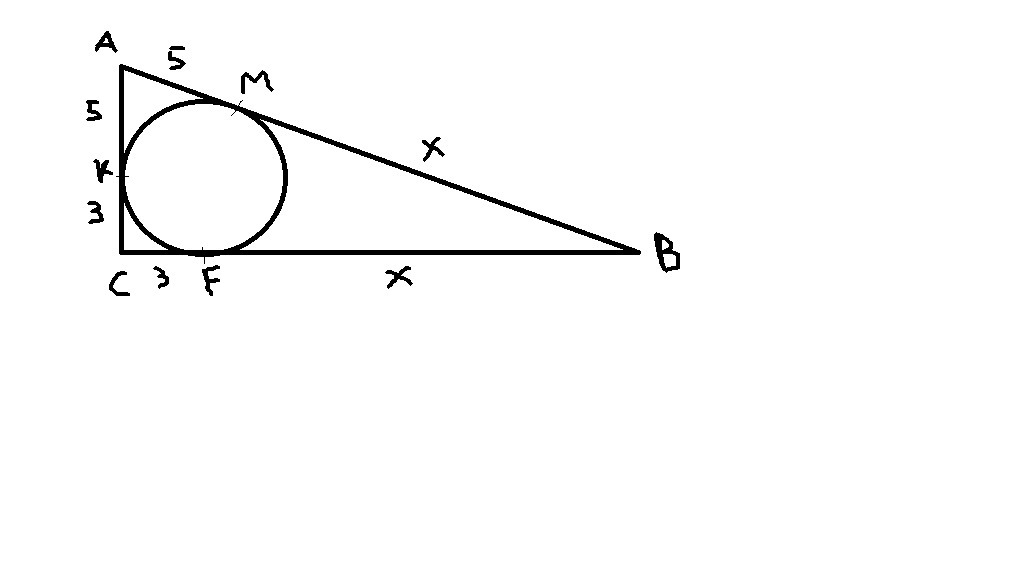
Не указано какой именно катет делит точка соприкосновения окружности, так что я намалевал в приложенном файле как будет выглядеть на мой взгляд.
Пусть там точка К делит катет АС на эти самые отрезки 3 и 5 см. Пусть АК=5см, СК=3см.
1) По свойству касательных АК=АМ=5см, СК=СF=3см, а BF=BM=x см.
Тогда AC=AK+CK=5+3=8 см, BC=CF+BF=3+x см, AB=AM+BM=5+x см.
2) По теореме Пифагора имеем AB²=AC²+BC²
(5+x)²=8²+(3+x)²
25+10x+x²=64+9+6x+x²
4x=48
x=12
Площадь прямоугольного треугольника это половина произведения катетов.
S=0.5*AC*BC=0.5*8*(3+12)=60 см.

Answer 2

Проверяем вместе что я понаписал)

Answer 3

Ой

Answer 4

я не площадь, а периметр написал)) ща поправлю

Answer 5

Большое спасибо

Answer 6

Теперь должно быть правильно. Если что, пишите, не выхожу пока что.