Предмет: Геометрия,
автор: vlamimikhaylin7387
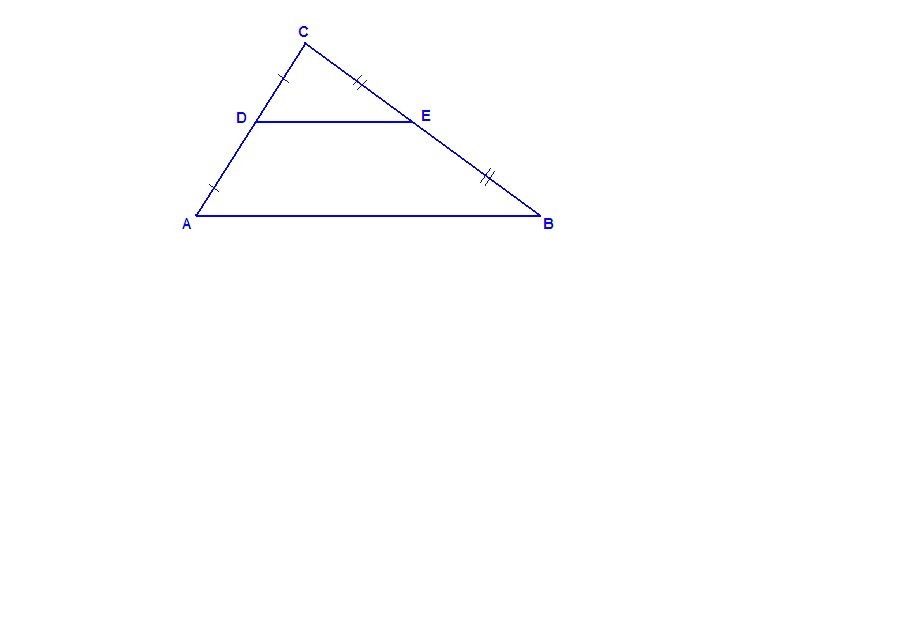
В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 12. Найдите площадь треугольника ABC.
Ответы
Автор ответа:
0
Средняя линия параллельна третьей стороне треугольника и равна ее половине:
DE║AB, DE = 1/2 AB.
∠CDE = ∠CAB как накрест лежащие углы при пересечении параллельных прямых DE и АВ секущей АС,
угол при вершине С общий для треугольников АВС и DEC, значит эти треугольники подобны по двум углам.
k = DE/AB = 1/2
Отношение площадей подобных треугольников равно квадрату коэффициента подобия:
Sdec : Sacb = k² = 1 : 4
Sabc = 4Sdec = 4 · 12 = 48
Приложения:
Похожие вопросы
Предмет: Физика,
автор: nazerkemufti08
Предмет: Математика,
автор: artemamidov755
Предмет: Химия,
автор: mazurleonid1711
Предмет: Математика,
автор: Arinochka1113
Предмет: История,
автор: Ольга042003