Question

диагональ равнобедренной трапеции перпендикулярна боковой стороне, которая равна 15 см,. Найдите площадь трапеции, если радиус описанной окружности = 12,5 см

Answer 1

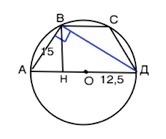
Если диагональ трапеции, вписанной в окружность, перпендикулярна боковой стороне, то ее большее основание - диаметр описанной окружности (см. рисунок).

Обозначим трапецию АВСД. Опустим высоту ВН. 

Треугольник АВД - прямоугольный, АН- проекция катета АВ на гипотенузу АД. 

АД=2R= 25 (см)

Катет - среднее пропорциональное между гипотенузой и проекцией катета на нее.

АВ²=АД•АН

АН=АВ²:АД=225:25=9 (см)

ВН=√(AB²-AH²)=√(225-81)=12 (см)

Высота равнобедренной трапеции, опущенная на большее основание,  делит его на отрезки, больший из которых равен средней линии трапеции. 

НД=25-9=16 (см)

Площадь трапеции равна произведению ее высоты на полусумму оснований, т.е. на среднюю линию. 

S (АВСД)=ВН•НД=12•16=192 см²