Предмет: Алгебра,
автор: Аолор
ПОМОГИТЕ ДАМ 30 БАЛЛОВ
Приложения:
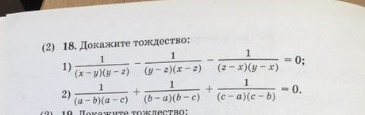
Ответы
Автор ответа:
0
Просто приводим к одному знаменателю


Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: azxdsadasddasd
Предмет: Литература,
автор: vladislavburluckiy
Предмет: Право,
автор: yuliagnatko
Предмет: Математика,
автор: nnsf