Предмет: Алгебра,
автор: hometown
Помогите решить хоть что-нибудь, пожалуйста!
Приложения:
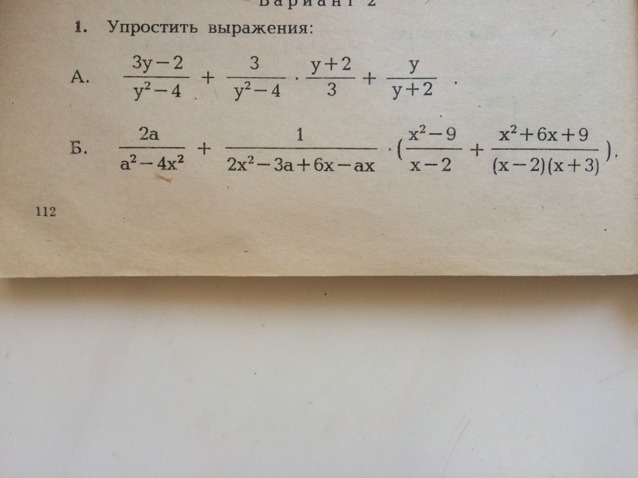
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: kkkkzkkkkkz
Предмет: История,
автор: badaevamilana1
Предмет: Қазақ тiлi,
автор: darinka123vitaminka
Предмет: Математика,
автор: superminepo
Предмет: Математика,
автор: kamella2005