2. Теоремы об углах, образованных двумя параллельными прямыми и секущей (формулировки и доказательство одной на выбор).
Ответы
Свойства параллельных прямых:
Если параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Если параллельные прямые пересечены секущей, то соответственные углы равны.
Если параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
Признаки параллельности прямых:
Если накрест лежащие углы, образованные при пересечении двух прямых секущей, равны, то эти прямые параллельны.
Если соответственные углы, образованные при пересечении двух прямых секущей, равны, то эти прямые параллельны.
Если сумма односторонних углов, образованных при пересечении двух прямых секущей, равна 180°, то эти прямые параллельны.
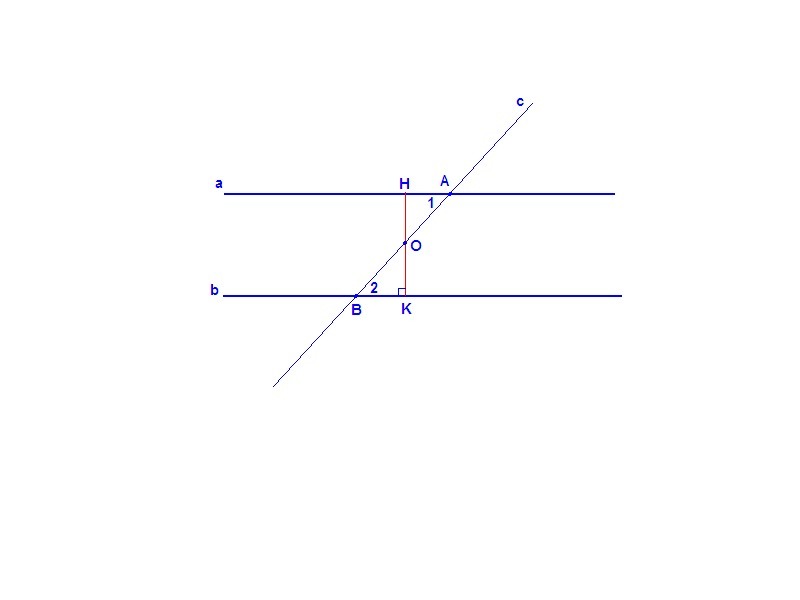
Доказательство 1-го признака:
Дано: с∩а, с∩b, ∠1 = ∠2.
Доказать: a║b.
Доказательство:
Пусть А и В - точки пересечения прямой с с прямыми а и b соответственно. О - середина отрезка АВ.
Проведем через точку О прямую КН перпендикулярную прямой b.
АО = ОВ, ∠1 = ∠2 по условию, ∠АОН = ∠ВОК как вертикальные, значит ΔАОН = ΔВОК по стороне и двум прилежащим к ней углам.
Значит ∠ВКО = ∠АНО = 90°, т.е. КН⊥b и КН⊥а, а если две прямые перпендикулярны третьей, то они параллельны, т.е. a║b.