Предмет: Геометрия,
автор: Hrisula
Параллелограммы ABCD и ADFE лежат в разных плоскостях.
Прямая m, параллельная BC, пересекает плоскости ABE и DFС соответственно в точках H и P. Докажите, что четырехугольник HPFE – параллелограмм
Ответы
Автор ответа:
0
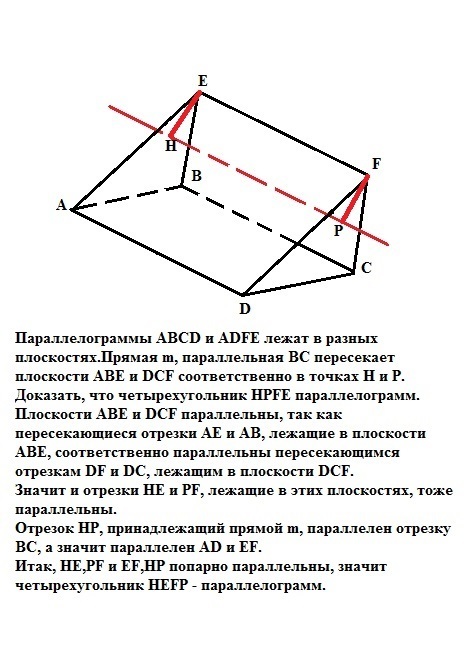
Параллелограммы АВСD и ADFE лежат в разных плоскостях.Прямая m, параллельная ВС пересекает плоскости АВЕ и DCF соответственно в точках Н и Р. Доказать, что четырехугольник НРFE параллелограмм.
Плоскости ABE и DCF параллельны, так как пересекающиеся отрезки AЕ и АВ, лежащие в плоскости АВЕ, соответственно параллельны пересекающимся отрезкам DF и DC, лежащим в плоскости DCF.
Значит и отрезки НЕ и РF, лежащие в этих плоскостях, тоже параллельны.
Отрезок НР, принадлежащий прямой m, параллелен отрезку ВС, а значит параллелен AD и EF.
Итак, НЕ,PF и EF,НР попарно параллельны, значит четырехугольник HEFP - параллелограмм.
Плоскости ABE и DCF параллельны, так как пересекающиеся отрезки AЕ и АВ, лежащие в плоскости АВЕ, соответственно параллельны пересекающимся отрезкам DF и DC, лежащим в плоскости DCF.
Значит и отрезки НЕ и РF, лежащие в этих плоскостях, тоже параллельны.
Отрезок НР, принадлежащий прямой m, параллелен отрезку ВС, а значит параллелен AD и EF.
Итак, НЕ,PF и EF,НР попарно параллельны, значит четырехугольник HEFP - параллелограмм.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Биология,
автор: polina4kazp
Предмет: Математика,
автор: springtimeandheat
Предмет: Математика,
автор: tsiiut
Предмет: Химия,
автор: Карина0089