Предмет: Математика,
автор: atgu228
Ребят, помогите решить производную первого порядка: (sqrt(1+3*x^2))/(2+3*x^2)
Приложения:
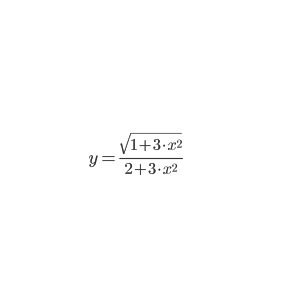
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Беларуская мова,
автор: fittingand
Предмет: Математика,
автор: Nika120410
Предмет: Геометрия,
автор: kate13kate
Предмет: Биология,
автор: slonikkk