Предмет: Математика,
автор: kabzyapparova
80 балл.
Срочно!
Упростить выражение и найти все значения x, при которых выражение принимает значение равное 2.
Приложения:
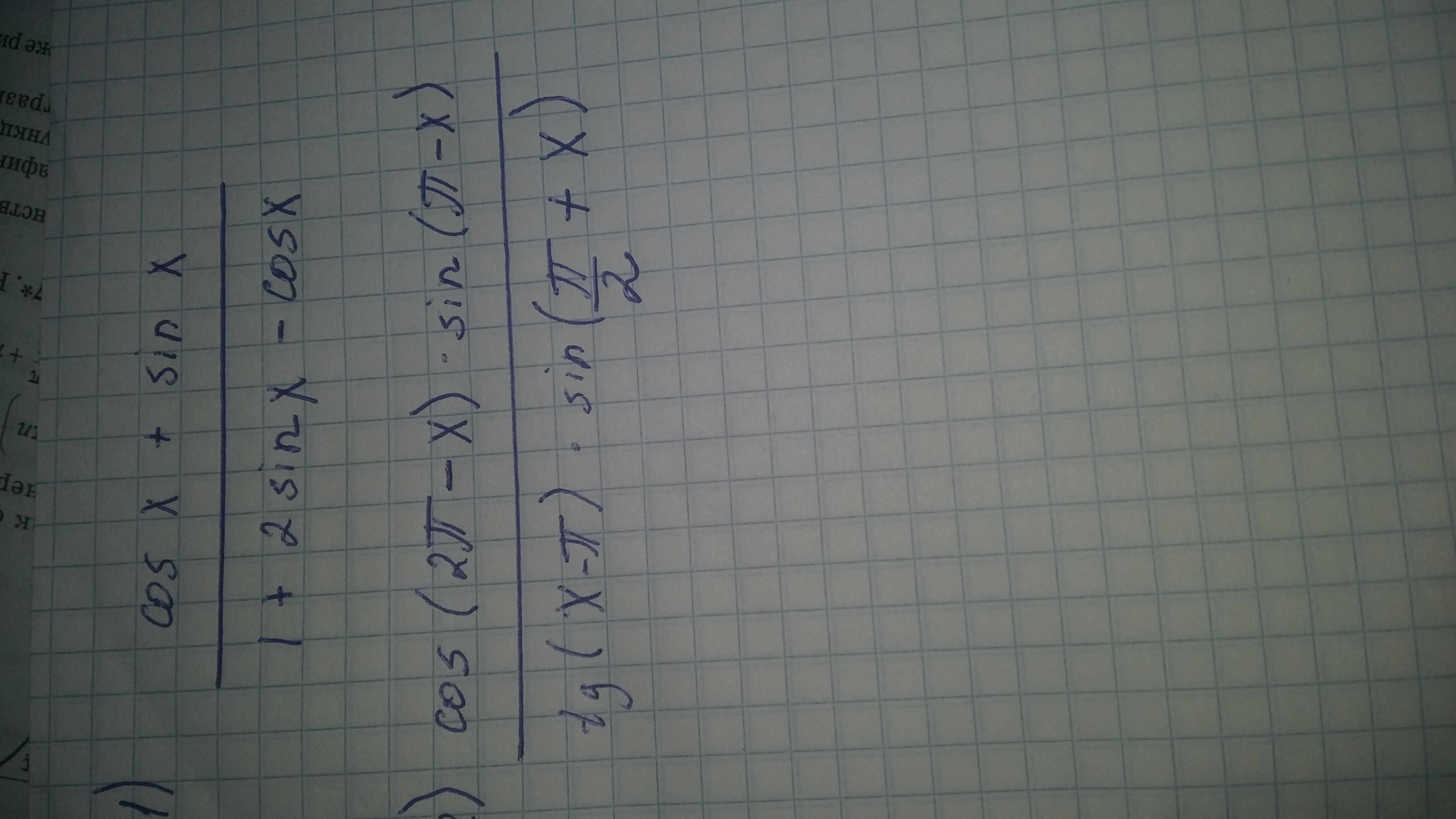
Ответы
Автор ответа:
0
Второе:
применим формулы приведения:
cosx · sinx / (tgx · cosx) = cosx · sinx / sinx = cosx
cos x = 2
нет корней.
Первое с таким условием:
(cosx + sinx) / (1 + 2sinx·cosx) =
= (cosx + sinx) / (sin²x + cos²x + 2sinx·cosx) =
= (cosx + sinx) / (sinx + cosx)² = 1 / (sinx + cosx)
1 / (sinx + cosx) = 2
sinx + cosx = 1/2
√2/2·sinx + √2/2·cosx =√2/4
sinx · cos(π/4) + cosx · sin(π/4) = √2/4
sin(x + π/4) = √2/4
x + π/4 = (-1)ⁿ · arcsin(√2/4) + πn
x = (-1)ⁿ · arcsin(√2/4) - π/4 + πn
применим формулы приведения:
cosx · sinx / (tgx · cosx) = cosx · sinx / sinx = cosx
cos x = 2
нет корней.
Первое с таким условием:
(cosx + sinx) / (1 + 2sinx·cosx) =
= (cosx + sinx) / (sin²x + cos²x + 2sinx·cosx) =
= (cosx + sinx) / (sinx + cosx)² = 1 / (sinx + cosx)
1 / (sinx + cosx) = 2
sinx + cosx = 1/2
√2/2·sinx + √2/2·cosx =√2/4
sinx · cos(π/4) + cosx · sin(π/4) = √2/4
sin(x + π/4) = √2/4
x + π/4 = (-1)ⁿ · arcsin(√2/4) + πn
x = (-1)ⁿ · arcsin(√2/4) - π/4 + πn
Автор ответа:
0
какое?
Автор ответа:
0
я добавила) к сожалению,не могу отправить ссылку
Автор ответа:
0
не могли бы вы посмотреть?
Автор ответа:
0
уравнение? смотрю
Автор ответа:
0
да,хорошо)
Похожие вопросы
Предмет: Русский язык,
автор: grypakis1983
Предмет: Английский язык,
автор: fozanmoran
Предмет: Физика,
автор: Foe1z
Предмет: Математика,
автор: Динка2004
Предмет: Математика,
автор: Ergalieva2003