Предмет: Геометрия,
автор: dashabelenko38
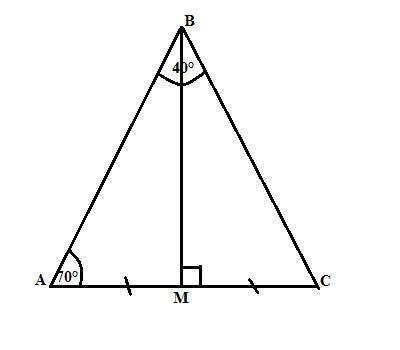
В треугольнике ABC точка M - середина стороны AC, ; угол BMA=90, угол ;ABC=40; угол BAM=70. Найдите углы MBC и BCM
Ответы
Автор ответа:
0
Ответ:
∠МВС = 20°.
∠ВСМ = 70°.
Объяснение:
В треугольнике АВС отрезок ВМ является и высотой (∠ВМА = 90° - дано) и медианой (точка М - середиеа стороны АС - дано). Следовательно, треугольник АВС равнобедренный с основанием АС и отрезок ВМ является биссектрисой (свойство). Тогда
∠МВС = ∠АВС:2 = 40:2 = 20°.
∠ВСМ = ∠ ВАМ = 70° (углы при основании равнобедренного треугольника).
Или так:
∠ВМА=∠ВМС=90° как смежные, равные в сумме 180°.
Прямоугольные треугольники АВМ и СВМ равны по двум катетам: ВМ - общий, а АМ = СМ (так как точка М - середина стороны АС - дано) Из равенства треугольников имеем равенство углов, лежащих против равных сторон:
∠МВС = ∠МВА = ∠АВС:2 = 40:2 = 20°. (∠АВС = ∠МВС + ∠МВА)
∠ВСМ = ∠ ВАМ = 70°.
Приложения:
Похожие вопросы
Предмет: География,
автор: zhasminkalieva900
Предмет: Русский язык,
автор: vladimirkuznecov0629
Предмет: Қазақ тiлi,
автор: li220994li
Предмет: Математика,
автор: papagreen
Предмет: История,
автор: AbbazovaAlina123