Предмет: Алгебра,
автор: Indomium
Найти точки ексремуму f'(x)=3x^2-2x-2
Ответы
Автор ответа:
0
Найдём сначала стационарные точки - это те точки, в которых производная равна нулю.
Приравниваем производную к нулю:

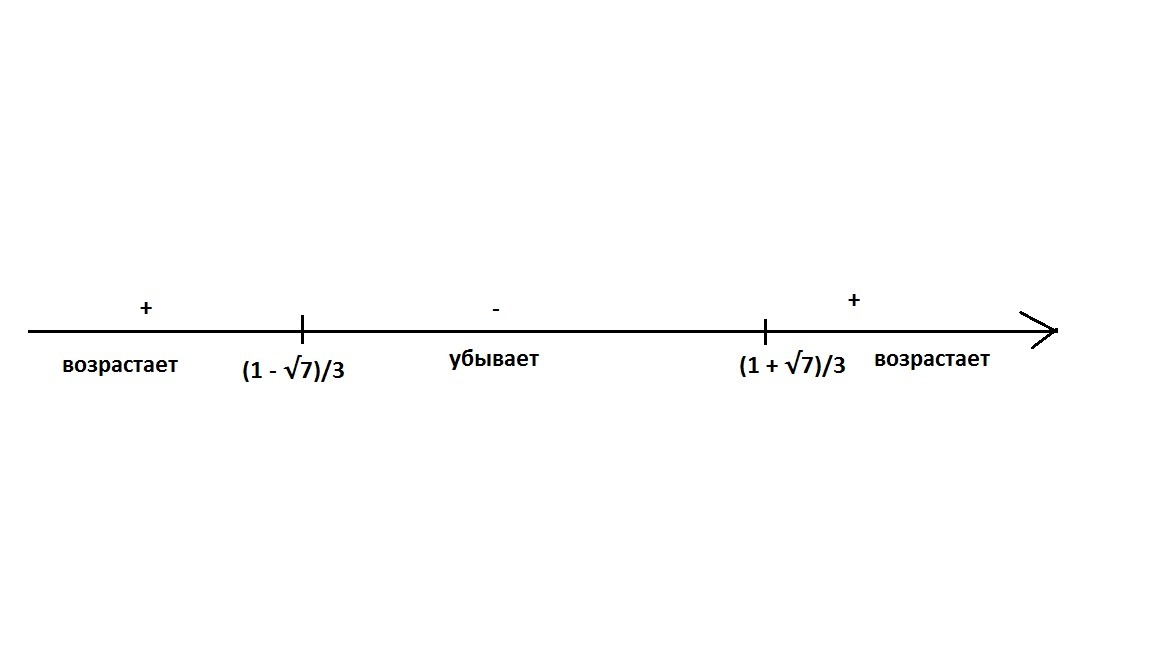
Найдём промежутки монотонности. Если в данных точках производная меняет свой знак, то данные точки будут являться точками экстремума.
Для этого решим неравенство:

Раз в данных точках убывание сменяется возрастанием и возрастание сменяется убыванием, то данные точки являются точками экстремума.
Приравниваем производную к нулю:
Найдём промежутки монотонности. Если в данных точках производная меняет свой знак, то данные точки будут являться точками экстремума.
Для этого решим неравенство:
Раз в данных точках убывание сменяется возрастанием и возрастание сменяется убыванием, то данные точки являются точками экстремума.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: jojopizzablabla
Предмет: История,
автор: sttyg556
Предмет: Русский язык,
автор: alibaba52
Предмет: Математика,
автор: лерочка72
Предмет: Химия,
автор: aaltynay