Предмет: Алгебра,
автор: Кентервильский1монах
Изобразите схематично график функции:
1) y=
2) y=
3)y=
4) y=
Ответы
Автор ответа:
0
Квадратичную функцию схематично можно построить по схеме:
1) определяем направление ветвей параболы;
2) находим координаты вершины параболы;
3) находим точки пересечения функции с осью ОХ;
4) находим точку пересечения функции с осью OY;
5) находим точку, симметричную точке пересечения с осью OY;
6) соединяем полученные точки плавной линией.
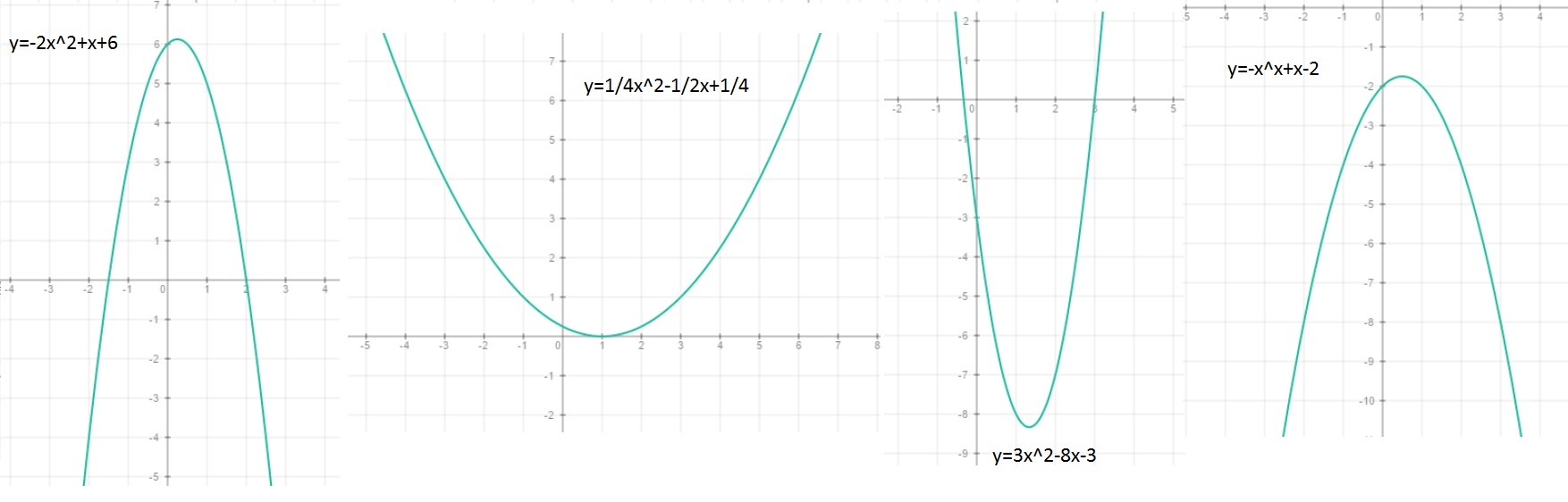
y=-2x²+x+6;
1) ветви параболы направлены вниз, так как а=-2<0;
2) x0=-b/(2a)=-1/-4=1/4;
y0=-2*(1/4)²+1/4+6=-1/8+1/4+6=6 ;
;
Вершина параболы ( ).
).
3) OX (y=0):
-2x²+x+6=0;
2x²-x-6=0;
D=1+48=49;
x1=(1-7)/4=-3/2;
x2=(1+7)/4=2;
Точки пересечения с осью ОХ: (-3/2;0), (2;0).
4) OY (x=0);
y=-2*0²+0+6=6;
Точка пересечения с осью OY: (0;6).
5) -2x²+x+6=6;
-2x²+x=0;
2x²-x=0;
x(2x-1)=0;
2x-1=0;
2x=1;
x=1/2.
Точка, симметричная точке (0;6) - (1/2;6).
6) см. на рисунке
y=1/4x²-1/2x+1/4;
1) ветви параболы направлены вверх, так как а=1/4>0;
2) x0=-b/(2a)=1/2/1/2=1;
y0=1/4*1²-1/2*1+1/4=1/4-1/2+1/4=0;
Вершина параболы (1;0).
3) OX (y=0):
1/4x²-1/2x+1/4=0;
x²-2x+1=0;
(x-1)²=0;
x=1
Точка пересечения с осью ОХ: (1;0).
4) OY (x=0);
y=1/4*0²-1/2*0+1/4=1/4;
Точка пересечения с осью OY: (0;1/4).
5) 1/4x²-1/2x+1/4=1/4;
x²-2x=0;
x(x-2)=0;
x-2=0;
x=2.
Точка, симметричная точке (0;1/4) - (2;1/4).
6) см. на рисунке
y=(2x-1)²-(x+2)²=(2x-1-x-2)(2x-1+x+2)=(x-3)(3x+1)=3x²+x-9x-3=3x²-8x-3;
1) ветви параболы направлены вверх, так как а=3>0;
2) x0=-b/(2a)=8/6=4/3;
y0=3*(4/3)²-8*4/3-3=16/3-32/3-3=-16/3-3=-8 1/3;
Вершина параболы (1 1/3;-8 1/3).
3) OX (y=0):
3x²-8x-3=0;
D=64+36=100;
x1=(8-10)/6=-1/3;
x2=(8+10)/6=3;
Точки пересечения с осью ОХ: (-1/3;0), (3;0).
4) OY (x=0);
y=3*0²-8*0-3=-3;
Точка пересечения с осью OY: (0;-3).
5) 3x²-8x-3=-3;
3x²-8x=0;
x(3x-8)=0;
3x-8=0;
3x=8;
x=8/3=2 2/3
Точка, симметричная точке (0;-3) - (2 2/3;-3).
6) см. на рисунке
y=-x²+x-2;
1) ветви параболы направлены вниз, так как а=-1<0;
2) x0=-b/(2a)=-1/-2=1/2;
y0=-(1/2)²+1/2-2=-1/4+1/2-2=-1 3/4;
Вершина параболы (1/2;-1 3/4).
3) OX (y=0):
-x²+x-2=0;
x²-x+2=0;
D=1-8=-7<0;
Точек пересечения с осью ОХ нет.
4) OY (x=0);
y=-0²+0-2=-2;
Точка пересечения с осью OY: (0;-2).
5) -x²+x-2=-2;
x²-x=0;
x(x-1)=0;
x-1=0;
x=1.
Точка, симметричная точке (0;-2) - (1;-2).
6) см. на рисунке
1) определяем направление ветвей параболы;
2) находим координаты вершины параболы;
3) находим точки пересечения функции с осью ОХ;
4) находим точку пересечения функции с осью OY;
5) находим точку, симметричную точке пересечения с осью OY;
6) соединяем полученные точки плавной линией.
y=-2x²+x+6;
1) ветви параболы направлены вниз, так как а=-2<0;
2) x0=-b/(2a)=-1/-4=1/4;
y0=-2*(1/4)²+1/4+6=-1/8+1/4+6=6
Вершина параболы (
3) OX (y=0):
-2x²+x+6=0;
2x²-x-6=0;
D=1+48=49;
x1=(1-7)/4=-3/2;
x2=(1+7)/4=2;
Точки пересечения с осью ОХ: (-3/2;0), (2;0).
4) OY (x=0);
y=-2*0²+0+6=6;
Точка пересечения с осью OY: (0;6).
5) -2x²+x+6=6;
-2x²+x=0;
2x²-x=0;
x(2x-1)=0;
2x-1=0;
2x=1;
x=1/2.
Точка, симметричная точке (0;6) - (1/2;6).
6) см. на рисунке
y=1/4x²-1/2x+1/4;
1) ветви параболы направлены вверх, так как а=1/4>0;
2) x0=-b/(2a)=1/2/1/2=1;
y0=1/4*1²-1/2*1+1/4=1/4-1/2+1/4=0;
Вершина параболы (1;0).
3) OX (y=0):
1/4x²-1/2x+1/4=0;
x²-2x+1=0;
(x-1)²=0;
x=1
Точка пересечения с осью ОХ: (1;0).
4) OY (x=0);
y=1/4*0²-1/2*0+1/4=1/4;
Точка пересечения с осью OY: (0;1/4).
5) 1/4x²-1/2x+1/4=1/4;
x²-2x=0;
x(x-2)=0;
x-2=0;
x=2.
Точка, симметричная точке (0;1/4) - (2;1/4).
6) см. на рисунке
y=(2x-1)²-(x+2)²=(2x-1-x-2)(2x-1+x+2)=(x-3)(3x+1)=3x²+x-9x-3=3x²-8x-3;
1) ветви параболы направлены вверх, так как а=3>0;
2) x0=-b/(2a)=8/6=4/3;
y0=3*(4/3)²-8*4/3-3=16/3-32/3-3=-16/3-3=-8 1/3;
Вершина параболы (1 1/3;-8 1/3).
3) OX (y=0):
3x²-8x-3=0;
D=64+36=100;
x1=(8-10)/6=-1/3;
x2=(8+10)/6=3;
Точки пересечения с осью ОХ: (-1/3;0), (3;0).
4) OY (x=0);
y=3*0²-8*0-3=-3;
Точка пересечения с осью OY: (0;-3).
5) 3x²-8x-3=-3;
3x²-8x=0;
x(3x-8)=0;
3x-8=0;
3x=8;
x=8/3=2 2/3
Точка, симметричная точке (0;-3) - (2 2/3;-3).
6) см. на рисунке
y=-x²+x-2;
1) ветви параболы направлены вниз, так как а=-1<0;
2) x0=-b/(2a)=-1/-2=1/2;
y0=-(1/2)²+1/2-2=-1/4+1/2-2=-1 3/4;
Вершина параболы (1/2;-1 3/4).
3) OX (y=0):
-x²+x-2=0;
x²-x+2=0;
D=1-8=-7<0;
Точек пересечения с осью ОХ нет.
4) OY (x=0);
y=-0²+0-2=-2;
Точка пересечения с осью OY: (0;-2).
5) -x²+x-2=-2;
x²-x=0;
x(x-1)=0;
x-1=0;
x=1.
Точка, симметричная точке (0;-2) - (1;-2).
6) см. на рисунке
Приложения:
Автор ответа:
0
Спасибо вам огромное!!!
Похожие вопросы
Предмет: Қазақ тiлi,
автор: majkenovaamina180
Предмет: Музыка,
автор: anastasiasmirnovahel
Предмет: Математика,
автор: sonaholodkova62
Предмет: Математика,
автор: nastyazhara
Предмет: Математика,
автор: AlinaLove111