Question

Срочно! Помогите, пожалуйста! Дана прямоугольная трапеция с острым углом 45° и большей боковой стороной, что равна 6√2 см. На расстоянии 4 см от плоскости трапеции лежит точка, равноудаленная от каждой стороны трапеции. Найдите расстояние от этой точки до сторон трапеции.

Answer 1

Данная точка вместе с вершинами трапеции образуют пирамиду в которой апофемы равны, значит основание высоты пирамиды лежит в центре вписанной в трапецию окружности, значит трапеция описанная. Для такой трапеции диаметр вписанной окружности равен её высоте. Так как трапеция прямоугольная, то её высота равна меньшей боковой стороне.

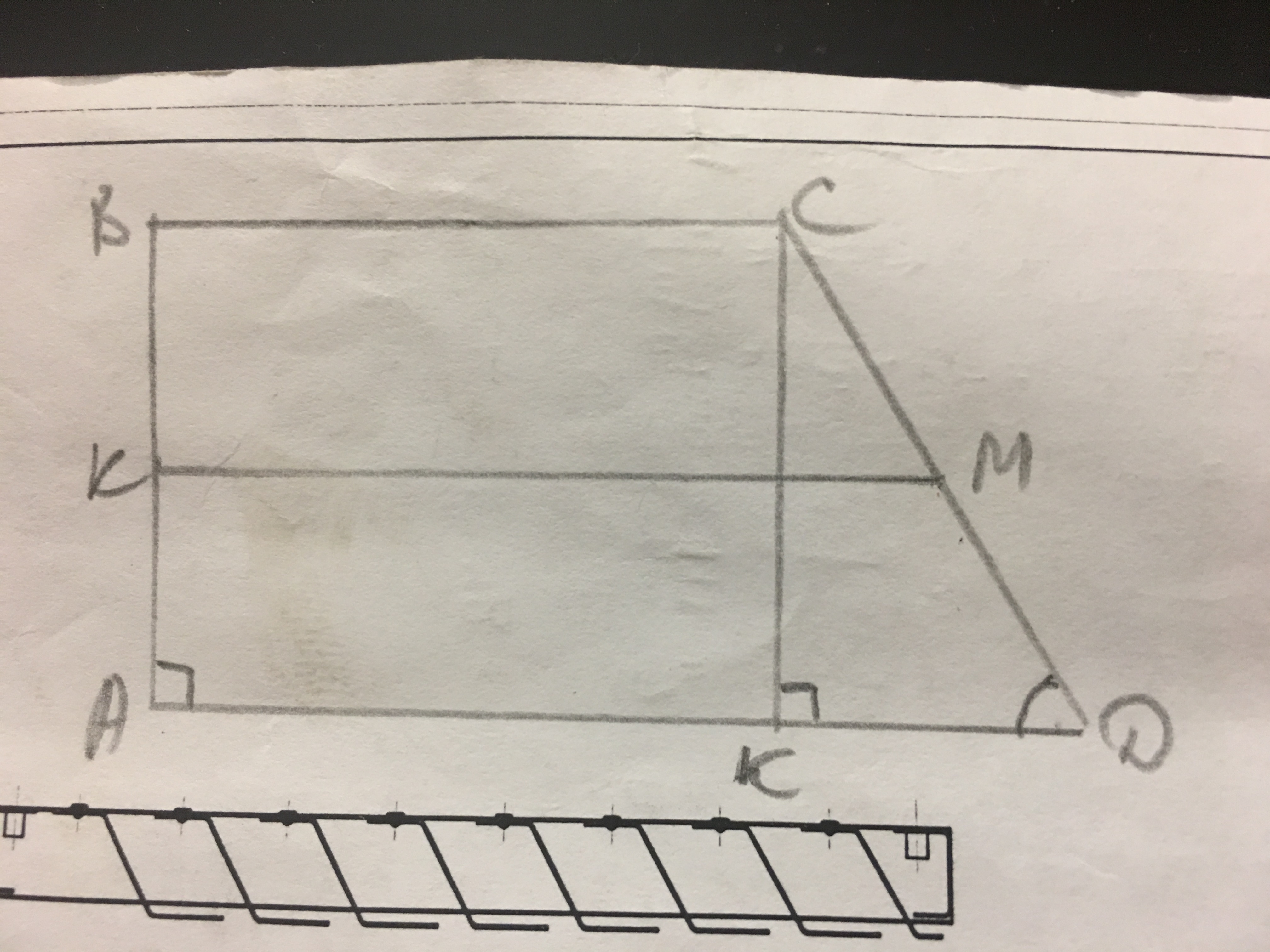
На схематично изображённой трапеции АВСД ∠Д=45°, значит тр-ник СДК равнобедренный, значит СК=СД/√2=6√2/√2=6 см.
Радиус вписанной окружности r=СК/2=3 см

В прямоугольном треугольнике, образованном высотой пирамиды, её апофемой и найденным радиусом, апофема по т. Пифагора равна:
l=√(h²+r²)=√(4²+3²)=5 см - это ответ.