Question

В равнобедренном треугольнике АВС точки К и М- середины его боковых сторон, а Ас- основание треугольника. КЕ и МД перпендикулярны к прямой АС. Докажите, что треугольники АКЕ и СМД равны.

Answer 1

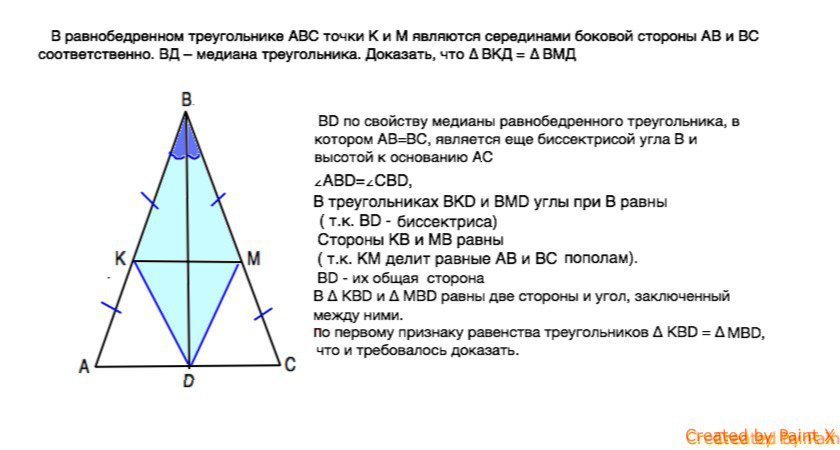
В равнобедренном треугольнике АВС точки К и М являются серединами боковой стороны АВ и ВС  соответственно. ВД – медиана треугольника. Доказать, что ∆ ВКД = ∆ ВМД

 ВД по свойству медианы равнобедренного треугольника, в котором АВ=ВС, является еще биссектрисой угла В и высотой к основанию АС

∠АВД=∠СВД,

В треугольниках ВКД и ВМД углы при В равны  ( ВД - биссектриса угла АВС) 

 Стороны КВ и МВ равны ( т.к. КМ делит равные АВ и ВС пополам). 

 ВД - их общая  сторона

В ∆ КВД и ∆ МВД равны две стороны и угол, заключенный между ними. 

По первому признаку равенства треугольников ∆ КВД = ∆ МВД, что и требовалось доказать.