Предмет: Алгебра,
автор: mkineshma
Помогите 7,8,9 пожалуйста)
Приложения:
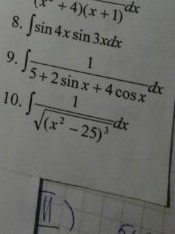
Ответы
Автор ответа:
0
8) преобразуем произведение в сумму (разность) по формуле:

выносим константу 1/2 за знак интеграла и берем его от каждого косинуса по отдельности:

9) Применяем основную тригонометрическую подстановку:


10) замена:



Теперь осталось выполнить обратную замену:


выносим константу 1/2 за знак интеграла и берем его от каждого косинуса по отдельности:
9) Применяем основную тригонометрическую подстановку:
10) замена:
Теперь осталось выполнить обратную замену:
Похожие вопросы
Предмет: Математика,
автор: muhammadik1209
Предмет: Литература,
автор: aruzhanriskalieva200
Предмет: Биология,
автор: sevcomsev
Предмет: Алгебра,
автор: жук234