Question

Косинус острого угла прямоугольной трапеции равен 3/корень из 13. Найдите её большее основание, если меньшее основание равно высоте и равно 24.

Answer 1

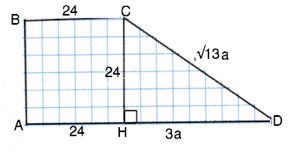
Пусть данная трапеция АВСD, отрезок СН – её высота. Так как АВСD прямоугольная трапеция, ВА⊥АD и СН⊥АD. ⇒ АВ=СН. По условию ВС=СН, ⇒ АВСН - квадрат. АН=ВС=СН=24. Косинус угла есть отношение катета, прилежащего углу, к гипотенузе. cos∠D=HD:CD

Примем коэффициент отношения НD:СD равным а. Тогда НD=3а, СD=а√13. Из прямоугольного ∆ СНD по т.Пифагора СН²=СD²-НD² 576=13а²-9а² ⇒ а=12, а НD=3а=36. Большее основание АD=AH+HD=24+36=60 (ед. длины).

Или:

СD=СН:sin∠D. Из основного тригонометрического тождества sin∠D=√(1-cos*D)=√(1-9/13)=2/√13 Гипотенуза СD=24:(2/√13)=12√13, откуда HD=CD•cos∠D=12√13•3:√13=36. Основание АD=24+36=60 (ед. длины)