Question

Найти площадь трапеции у которой основания равны 142 см и 89 см, диагонали 120 см и 153 см.

Answer 1

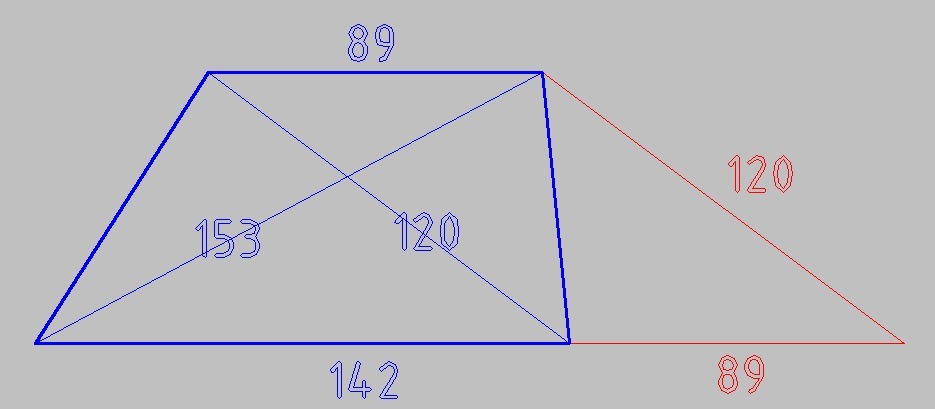
Достроим справа к нашей трапеции вспомогательные линии - к нижнему основанию отрезок 89 см, равный верхнему основанию и отрезок, параллельный диагонали в 120 см. НА рисунке эти вспомогательные линии красные.
Площадь трапеции - полусумма оснований на высоту
S = 1/2(a+b)*h
a = 142 см
b = 89 см
S = 231h/2
Площадь треугольника - половина произведения основания треугольника, равного а+b = 231 см на высоту
S = 1/2(a+b)*h
S = 231h/2
Площади совпадают
Вычислим площадь треугольника со сторонами 153, 120 и 142+89 = 231 см по формуле Герона
Полупериметр
p = (153 + 120 + 231)/2 = 252 см
Площадь
S² = p(p-a)(p-b)(p-c)
S² = 252(252-153)(252-120)(252-231)
S² = 69155856
S = 8319 см²