Перерізи кулі двома паралельними площинами , між якими лежить центр кулі мають площі 144пі см , 25пі см. Знайти площу поверхні кулі, якщо відстань між паралельними площинами дорівнює 17 см
Ответы
Сечения шара двумя параллельными плоскостями, между которыми лежит центр шара, имеют площади 144π см, 25π см. Найти площадь поверхности шара, если расстояние между параллельными плоскостями равен 17 см
* * *
Сечение шара плоскостью - круг.
Расстояние между плоскостями равно длине перпендикуляра, опущенного с одной плоскости на другую.
Центр шара и центры сечений параллельными плоскостями лежат на одной прямой.
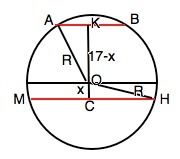
На схематическом рисунке приложения – сечение шара через его центр О и центры сечений.
АК- радиус меньшего сечения, СН - радиус большего сечения, СК - расстояние между центрами сечений, ОА=ОН - радиус шара.
Квадрат радиуса меньшего сечения АК²=S1:π=25
Квадрат радиуса большего сечения СН²=S2:π=144
Обозначим расстояние между центром шара и большим сечением СО=х, тогда между центром шара и меньшим сечением ОК=17-х.
Из ∆ АОК по т.Пифагора
R²=АК²+ОК²
Из СОН
R²=CH²+CO²
Приравняем оба значения R²:
АК²+ОК²=CH²+CO²
25+289-34х+х²=144+х*
34х=170
х=5
R²=ОН²=25+144=169
Формула площади поверхности шара
S=4πR²
S=4π•169=676π см²