Предмет: Физика,
автор: ilyakiev
Определить действующее значение тока
Приложения:
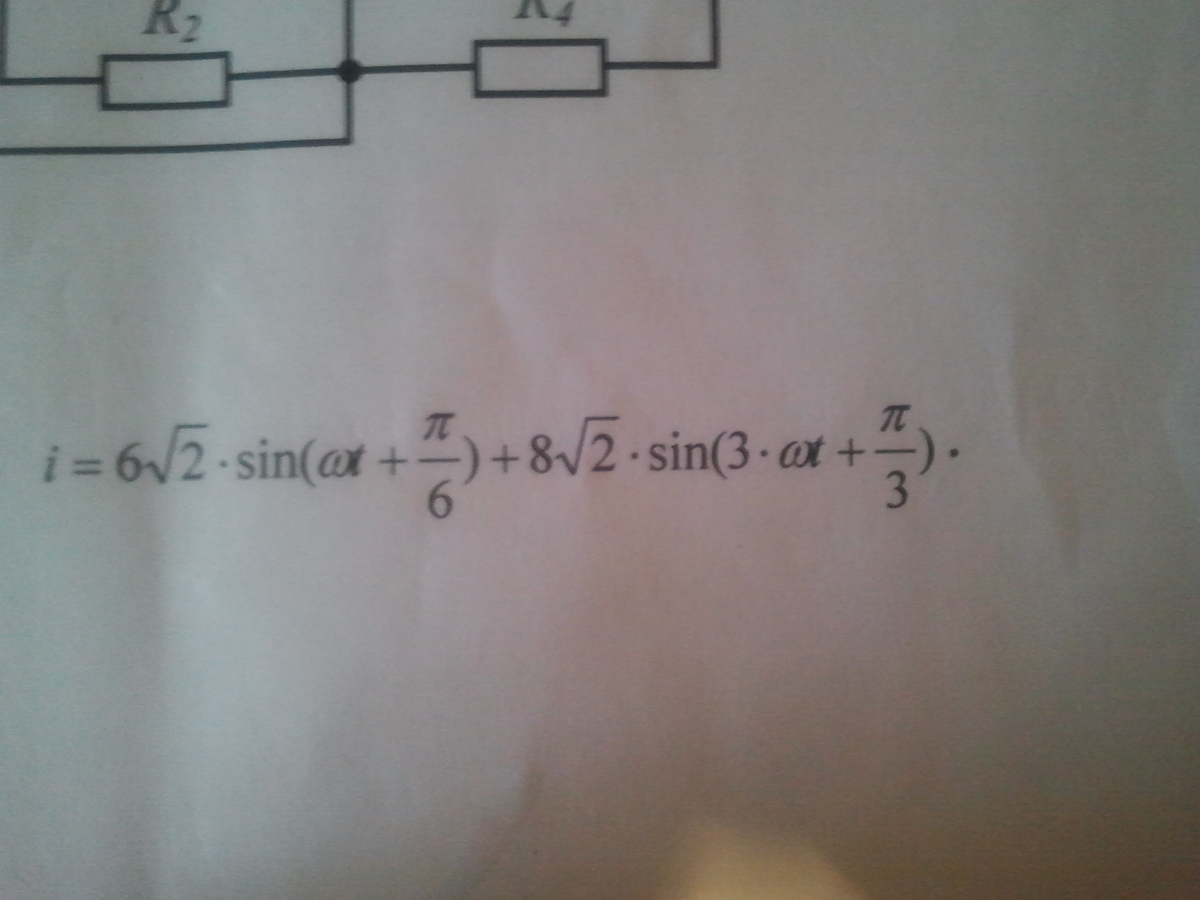
Ответы
Автор ответа:
0
Действующее значение синусоидального тока, определяется как средне квадратичное за период:

Находим значения интегралов:
Первая часть:

Вторая часть:

Третья часть:

Получаем:

Так как синус, в подстановках одного периода![[0;pi] [0;pi]](https://tex.z-dn.net/?f=%5B0%3Bpi%5D) принимает нулевые значения, получаем:
принимает нулевые значения, получаем:

Ответ: действующее значение силы тока равно 100А
Находим значения интегралов:
Первая часть:
Вторая часть:
Третья часть:
Получаем:
Так как синус, в подстановках одного периода
Ответ: действующее значение силы тока равно 100А
Похожие вопросы
Предмет: Математика,
автор: mysaevrahidin8
Предмет: Английский язык,
автор: Zxcv0011
Предмет: География,
автор: gens2008gens2008
Предмет: Физика,
автор: gangster5
Предмет: Литература,
автор: Andrew4343