Предмет: Алгебра,
автор: знаток12345
Найти наибольшее значение функции y=sin^2(2x) / sin^4(x)+cos^4(x)
Приложения:
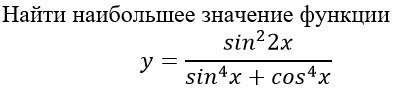
Ответы
Автор ответа:
0
В точке экстремума y' = 0.
sin 4x = 0
4x = πn, n ∈ Z
x = πn/4, n ∈ Z
Среди этих экстремумов максимумы: x = π/4 + πn/2, n ∈ Z.
Максимальное значение функции:
Автор ответа:
0
спасибо за проделанную работу
Похожие вопросы
Предмет: История,
автор: sevaranaverdinovna
Предмет: Қазақ тiлi,
автор: Nikita15680
Предмет: Кыргыз тили,
автор: mihajlukilaria
Предмет: Математика,
автор: Вика123991
Предмет: Математика,
автор: Ученикдарына