Question

Ребята помогите 443, 444 задачи

Answer 1

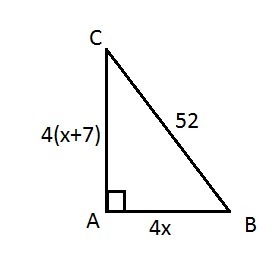
443. Так как велосипедисты двигаются по перпендикулярным лучам, рассмотрим прямоугольный треугольник АВС с прямым углом А. (см. рисунок)
Пусть точка А - отправной пункт двух велосипедистов. Точка В - пункт велосипедиста с меньшей скоростью через 4 часа, а точка С - пункт велосипедиста с большей скоростью через 4 часа.
Пусть х - меньшая скорость, тогда (х+7) - большая скорость, 4х - расстояние, которое проехал велосипедист с меньшей скоростью за 4 часа (расстояние АВ), 4(х+7) - расстояние, которое проехал велосипедист с большей скоростью за 4 часа (расстояние АС). Расстояние между ними через 4 часа 52 км. По т.Пифагора:
(4x)²+(4(x+7))²=52²;
16x²+16(x²+14x+49)=2704; |:16
x²+x²+14x+49=169;
2x²+14x-120=0; |:2
x²+7x-60=0;
D=49+240=289;
x1=(-7-17)/2=-12;
x2=(-7+17)/2=5.
Так как скорость - величина положительная, то меньшая скорость равна 5 км/ч, а большая скорость 5+7=12 км/ч.
Ответ: 5 км/ч, 12 км/ч.
 
444. Пусть скорость катеров равна V км/ч (она у катеров одинаковая), скорость течения одной реки - V1 км/ч, а скорость другой реки - V2 км/ч, причем V1>V2. Обозначим через S - расстояние в одном направлении, тогда один катер проходит расстояние туда и обратно за время
$t_{1}= frac{S}{V-V1}+ frac{S}{V+V1}= frac{2SV}{V^2-V1^2}.$
Второй катер проходит расстояние туда и обратно за время
$t_{2}= frac{S}{V-V2}+ frac{S}{V+V2}= frac{2SV}{V^2-V2^2}.$
Числители у обеих дробей одинаковые (2SV), а из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше. Так как скорость V1>V2, то знаменатель первой дроби меньше знаменателя второй дроби. Таким образом, больше времени потребуется в реке с более быстрым течением.
Ответ: в реке с более быстрым течением.

Answer 2

большое спасибо ))

Answer 3

только вперед !!! умница