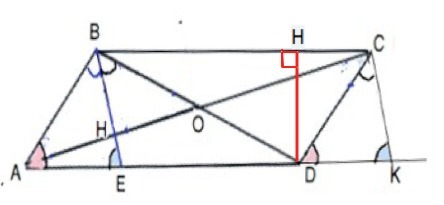
В параллелограмме ABCD биссектриса BE угла ABD перпендикулярна диагонали AC и равна 1/4AC. Найдите стороны параллелограмма если известно, что BE=6.
Ответы
решение в приложении
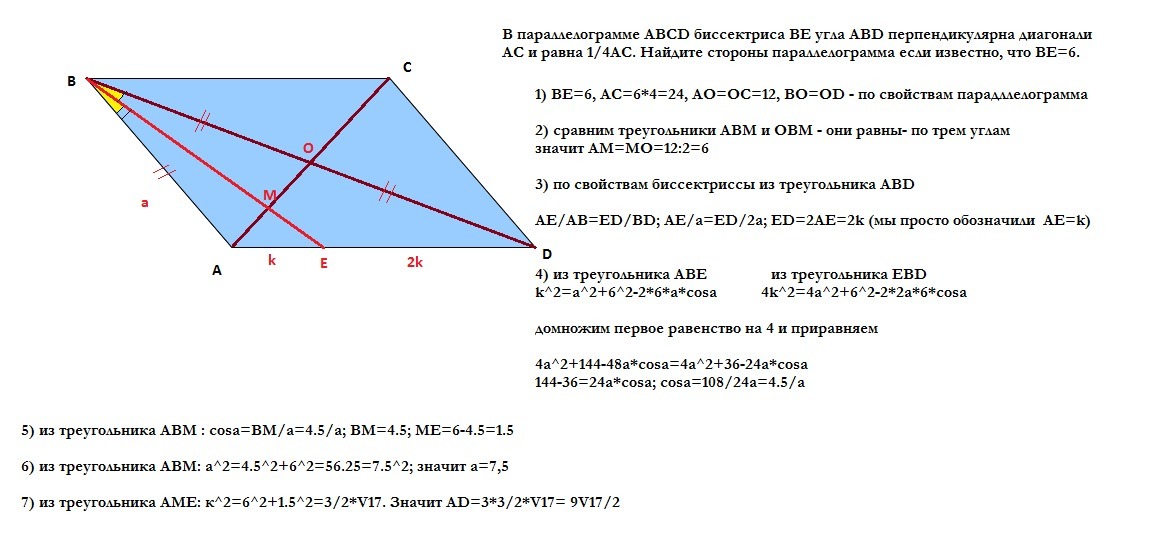
ВЕ=АС/4=6 ⇒ АС=6•4=24
Пусть О - т.пересечения диагоналей.
Диагонали параллелограмма делятся пополам.
АО=24:2=12
Обозначим Н точку пересечения ВЕ и АО
В ∆ АВО биссектриса ВН перпендикулярна основанию АО. ⇒ ВЕ - высота.
Если биссектриса треугольника совпадает с высотой, этот треугольник равнобедренный, поэтому ВН - медиана, и АН=НО=6
Проведем СК║ВЕ.
АD=BC, ЕК=ВС. ⇒
Параллелограммы АВСD и ВСКЕ равновелики -
высота DH параллелограммов и сторона, BC, к которой эта высота проводится - общие.
S АВСD=S BCKE
В параллелограмме ВСКЕ НС⊥ВЕ.⇒ НС - его высота.
Ѕ (ВСКЕ)=СН•ВЕ=18•6=108 =Ѕ(ABCD)
Диагональ параллелограмма делит его на два равных треугольника.
Ѕ ∆ АВС=Ѕ АВСD:2=54⇒
BH=2S∆ ABC:2=108:24=4,5
Из прямоугольного ∆ АВС по т.Пифагора
АВ=√(АН²+ВН²)=√56,25=7,5
Из прямоугольного ВНС по т.Пифагора
ВС=√(CH²+BH²)=√344,25=4,5√17
АВ=CD=7,5; AD=BC=4,5√17