Предмет: Алгебра,
автор: sas47
первый и второй с решением!
Приложения:
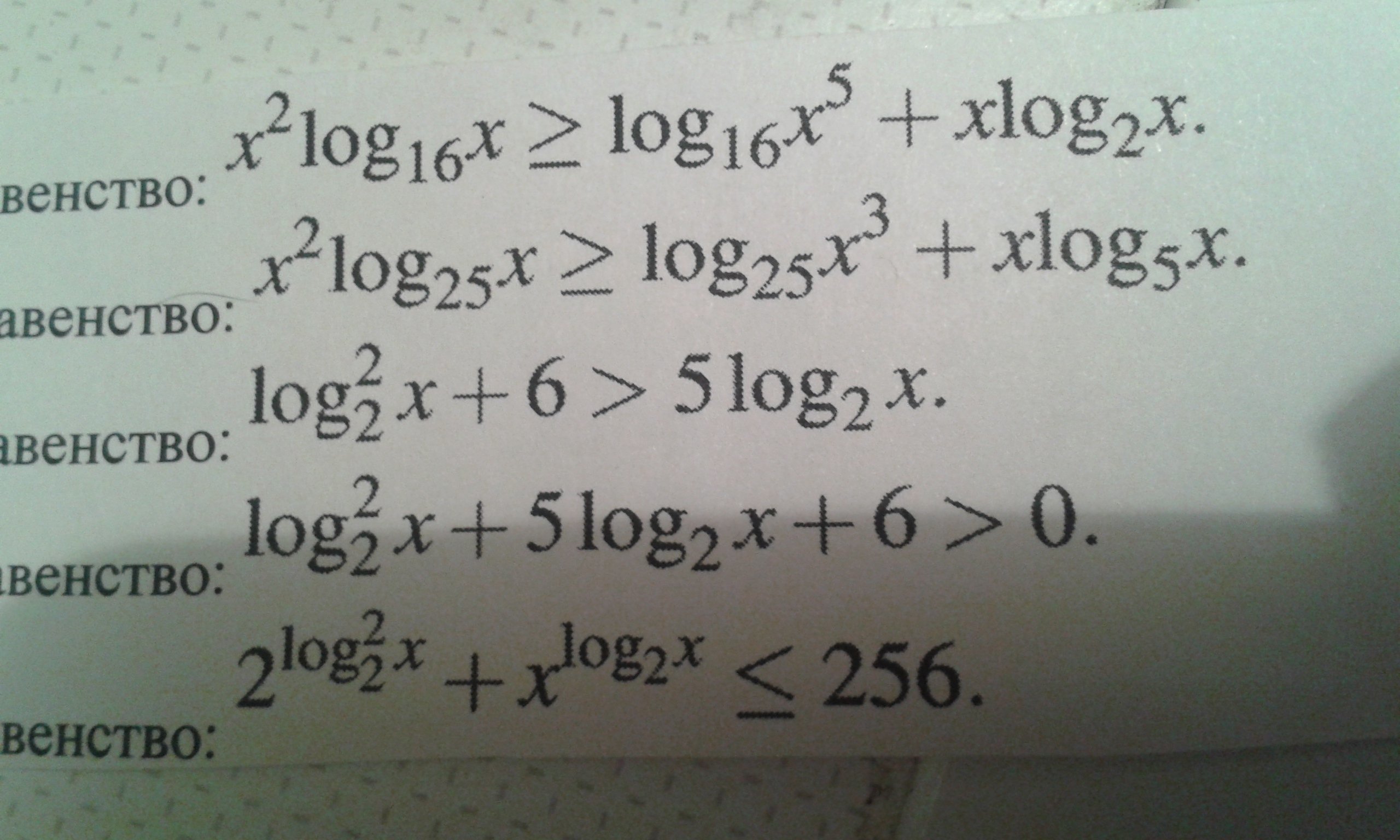
Ответы
Автор ответа:
0
1) log₁₆x = log₂x/log₂16 = log₂x/4
x > 0
теперь сам пример:
х²*log₂x/4 ≥ 5*log₂x/4 + xlog₂x | *4
x²log₂x ≥ 5log₂x +4xlog₂x
x²log₂x - 5log₂x - 4xlog₂x ≥ 0
log₂x (x² -5 - 4x) ≥0
метод интервалов.
log₂x =0 x² -5 - 4x = 0
х = 1 х = 5, х = -1
-∞ -1 0 1 5 +∞
- + + это знаки log₂x
+ - - - + это знаки x² -5 - 4x
IIIIIIIIIII IIIIIIIIIIIIIII это решение
2)log₂₅x = log₅x/2
x > 0
теперь сам пример:
х²log₅x/2 ≥ 3 log₅x/2 + xlog₅x | * 2
х²log₅x ≥ 3 log₅x + 2xlog₅x
х²log₅x - 3 log₅x - 2xlog₅x ≥ 0
log₅x(x² - 3 - 2x) ≥ 0
метод интервалов
log₅x = 0
х = 1 x² - 3 - 2x = 0
х = -1 х = 3
-∞ -1 0 1 3 +∞
- + + это знаки log₅x
+ - - - + это знаки x² - 3 - 2x
IIIIIIIIIIIIII IIIIIIIIIIIIIIIIIIII это решение
x > 0
теперь сам пример:
х²*log₂x/4 ≥ 5*log₂x/4 + xlog₂x | *4
x²log₂x ≥ 5log₂x +4xlog₂x
x²log₂x - 5log₂x - 4xlog₂x ≥ 0
log₂x (x² -5 - 4x) ≥0
метод интервалов.
log₂x =0 x² -5 - 4x = 0
х = 1 х = 5, х = -1
-∞ -1 0 1 5 +∞
- + + это знаки log₂x
+ - - - + это знаки x² -5 - 4x
IIIIIIIIIII IIIIIIIIIIIIIII это решение
2)log₂₅x = log₅x/2
x > 0
теперь сам пример:
х²log₅x/2 ≥ 3 log₅x/2 + xlog₅x | * 2
х²log₅x ≥ 3 log₅x + 2xlog₅x
х²log₅x - 3 log₅x - 2xlog₅x ≥ 0
log₅x(x² - 3 - 2x) ≥ 0
метод интервалов
log₅x = 0
х = 1 x² - 3 - 2x = 0
х = -1 х = 3
-∞ -1 0 1 3 +∞
- + + это знаки log₅x
+ - - - + это знаки x² - 3 - 2x
IIIIIIIIIIIIII IIIIIIIIIIIIIIIIIIII это решение
Похожие вопросы
Предмет: Геометрия,
автор: MarikaBy
Предмет: Химия,
автор: anasssssssstasiawshw
Предмет: Геометрия,
автор: tanvadim2
Предмет: Алгебра,
автор: dimalex4116
Предмет: Литература,
автор: Аноним