Question

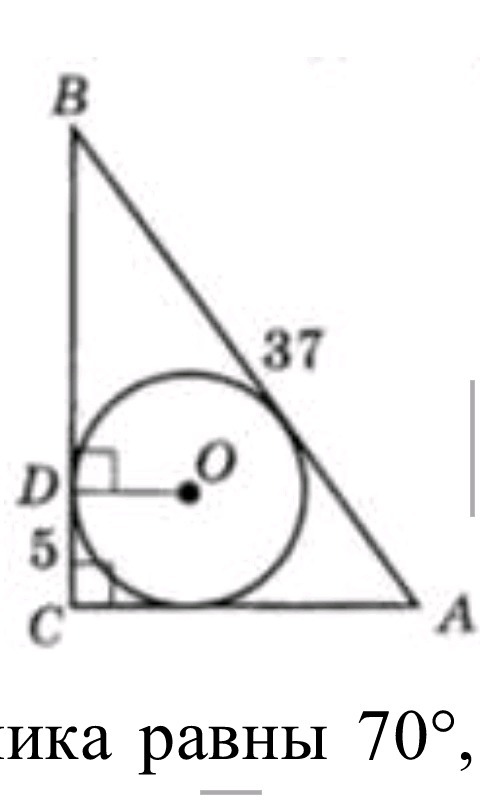
На рисунке точка О – центр вписанной окружности, CD = 5 см, АВ = 37 см. Найдите SАВС.

Answer 1

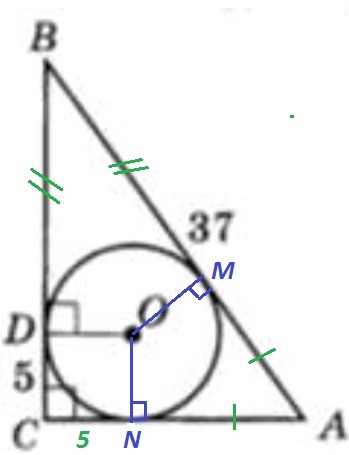
Дано:  ΔABC  прямоугольный, ∠С = 90°; AB = 37; CD = 5; OD⊥BC

Проведём радиус ON⊥AC. Радиус в точку касания образует прямой угол с касательной в эту точку. Получился квадрат CDON.  Значит, радиус вписанной окружности    r = ON = CD = 5

Отрезки касательных к окружности, проведённые из одной точки, равны между собой  ⇒

AM = AN;    BM = BD;    CN = CD = 5

AB = 37 = AM + BM = AN + BD

Периметр треугольника ABC :

P = (CD + CN) + (AN + BD) + AB = (5 + 5) + 37 + 37 = 84

Полупериметр треугольника АВС : p = 84/2 = 42

Площадь треугольника равна произведению полупериметра на радиус вписанной окружности :

$S_{ABC}=rp = 5 cdot 42 = 210$

S = 210