Предмет: Алгебра,
автор: dashkadashulya
Помогите, пожалуйста!
Приложения:
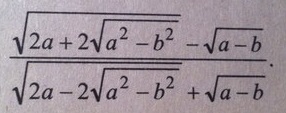
Ответы
Автор ответа:
0
a+b>=0, a-b>=0
a>=-b, a>=b --->
Похожие вопросы
Предмет: Химия,
автор: ndnsjdbdbej
Предмет: Биология,
автор: log567123
Предмет: Литература,
автор: monikatodua624
Предмет: Физика,
автор: Andrey0812
Предмет: Физика,
автор: wkolnik1337