Предмет: Геометрия,
автор: TvoyGolovnoyMozg
В остроугольном треугольнике ABC на сторонах АС и ВC отмечены соответственные точки N и L так, что NL параллельна AB и NL=LB; На стороне AB отмечена точка M так, что что угол LMB = углу ACB. Найдите CN, если LM=5 С чертежом, пожалуйста.
Ответы
Автор ответа:
0
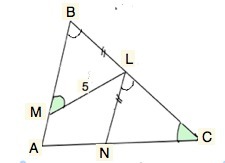
Сделаем рисунок.
По условию ВL=LN,
LN||AC
Рассмотрим ∆ BML и ∆ CNL
Углы ВМL = NCL ( т.к. он равен АСВ)
углы МВL=NLC - равные соответственные при пересечении параллельных LN||AC секущей ВС.
∆ BML подобен ∆CNL по двум равным углам.
Следовательно, их третьи углы тоже равны.
Тогда эти треугольники не только подобны, но и равны, так как имеют по равной стороне ВL=LN и прилежащим к ней углам.
Значит, CN равна ML и равна 5
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: akabaevaf
Предмет: Физкультура и спорт,
автор: tvprowill
Предмет: Математика,
автор: adildusupov40
Предмет: Информатика,
автор: korolmaus1
Предмет: Математика,
автор: mauser88