Предмет: Математика,
автор: mishganoff
Решите неравенство log_2/3(2-5x)<-2
Приложения:
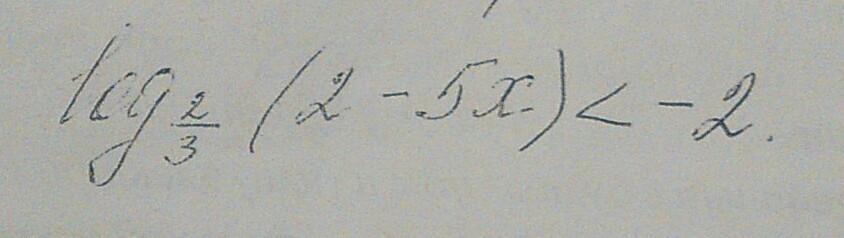
Ответы
Автор ответа:
0
Решение смотри на фото
Приложения:
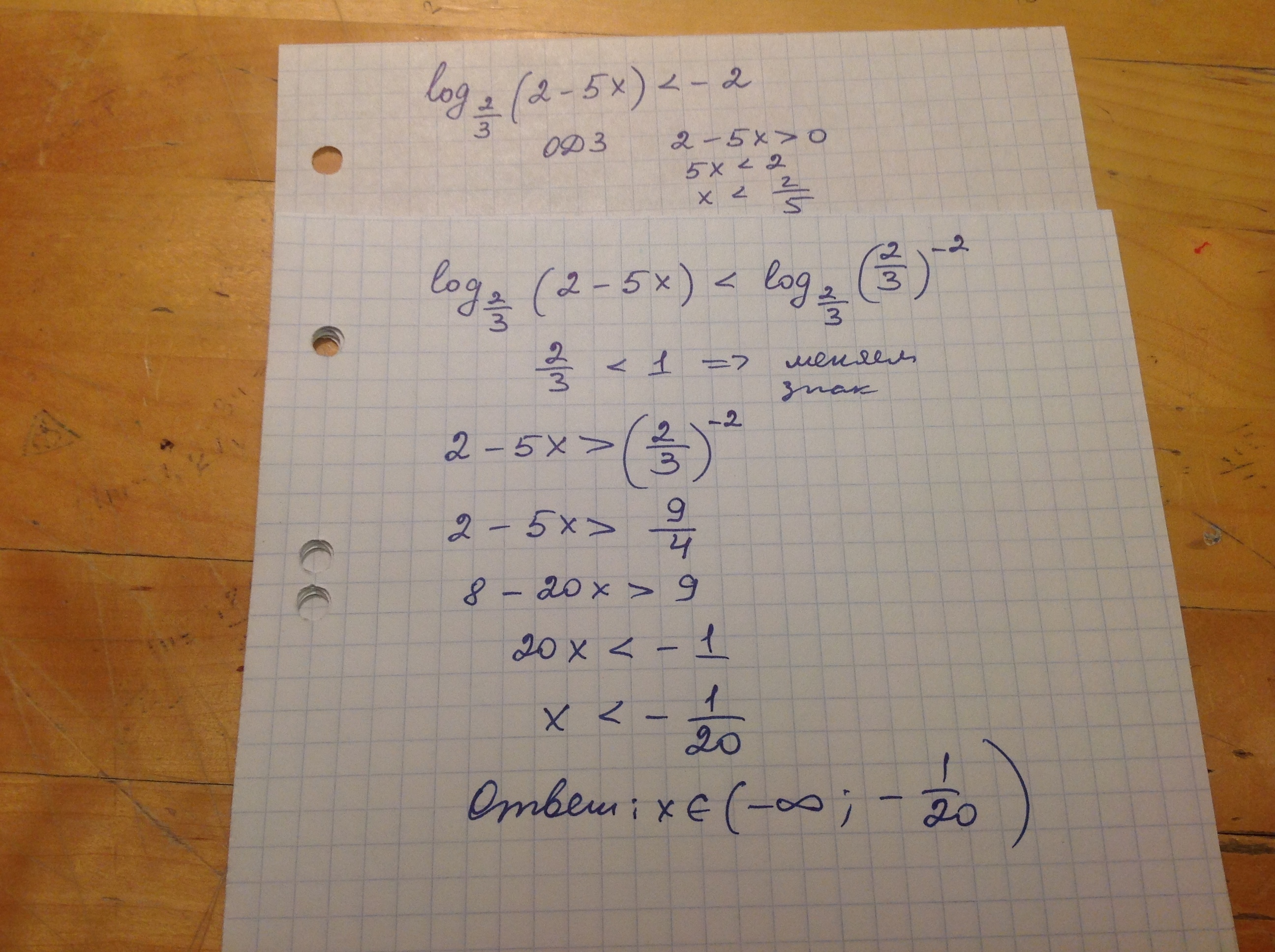
Автор ответа:
0
а как на бумаги можно написать?
Автор ответа:
0
сфоткай и скинь вопросом
Автор ответа:
0
я сфоткал ну а как скинуть?
Автор ответа:
0
задай вопрос там можно скинуть
Автор ответа:
0
а вопрос скинь мне в эти коменты
Автор ответа:
0
Решите неравенство Loq_2/3 (2 -5x) < -2 ;
--------
Основание логарифма 0 < 2/3 < 1 , значит логарифмическая функция убывающая , поэтому :
Loq_2/3 (2 -5x) < - 2 ⇔
2 - 5x > (2/3)⁻² ; * * * (2/3)⁻² = 1 / (2/3)² =1 / 4/9 = 9/4 > 0 * * *
2 - 5x > 9 / 4 ;
2 - 9/ 4 > 5x ;
-1/4 > 5x ;
-1 / 20 > x .
ответ : x ∈ ( - ∞ ; - 0, 05 ) .
--------
Основание логарифма 0 < 2/3 < 1 , значит логарифмическая функция убывающая , поэтому :
Loq_2/3 (2 -5x) < - 2 ⇔
2 - 5x > (2/3)⁻² ; * * * (2/3)⁻² = 1 / (2/3)² =1 / 4/9 = 9/4 > 0 * * *
2 - 5x > 9 / 4 ;
2 - 9/ 4 > 5x ;
-1/4 > 5x ;
-1 / 20 > x .
ответ : x ∈ ( - ∞ ; - 0, 05 ) .
Приложения:
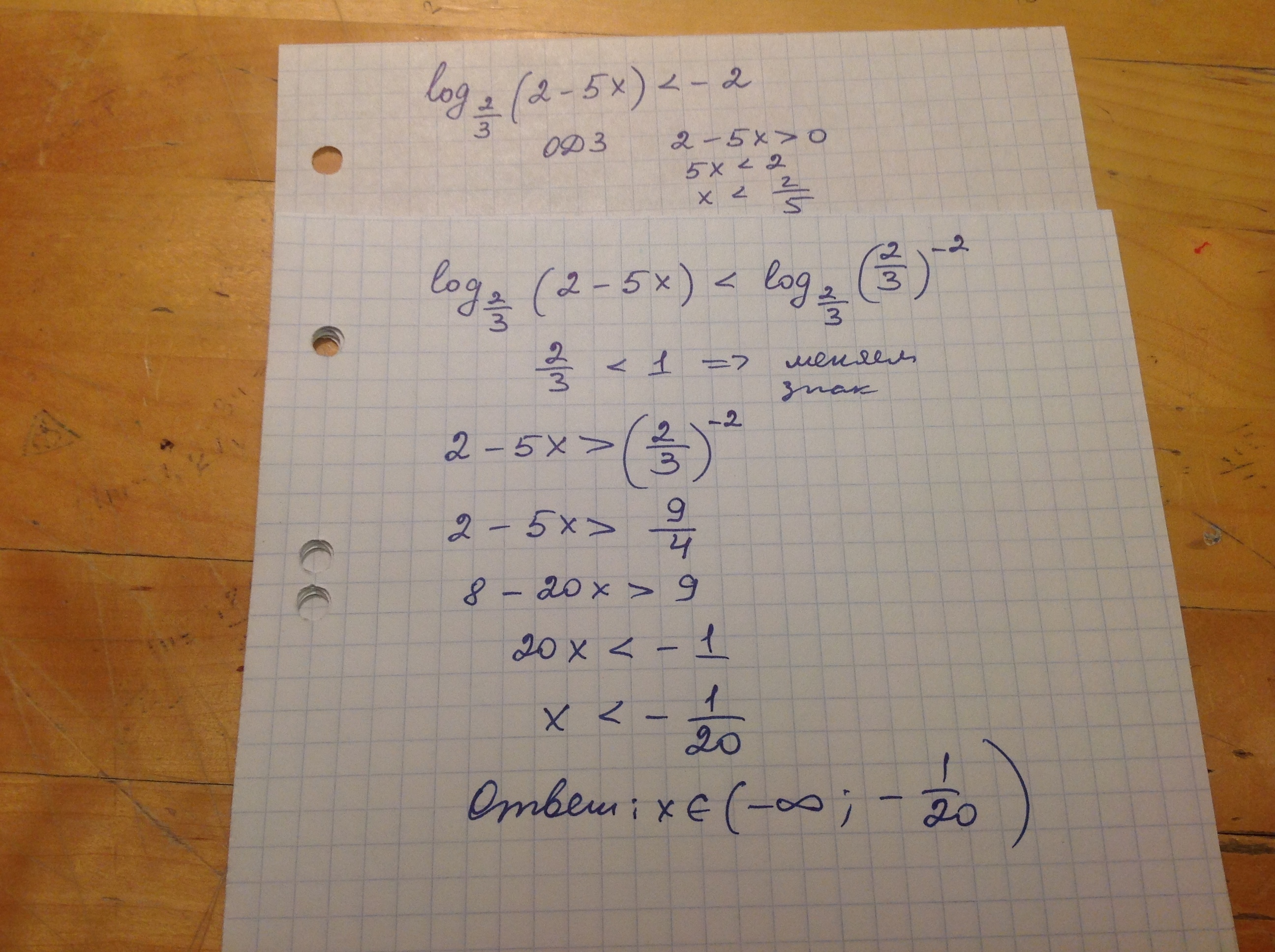
Похожие вопросы
Предмет: Алгебра,
автор: elenagilbertsal
Предмет: Қазақ тiлi,
автор: batyryersin
Предмет: Информатика,
автор: wqqqt
Предмет: Математика,
автор: Katyakata
Предмет: Литература,
автор: bulcetin631