Предмет: Геометрия,
автор: obyava12
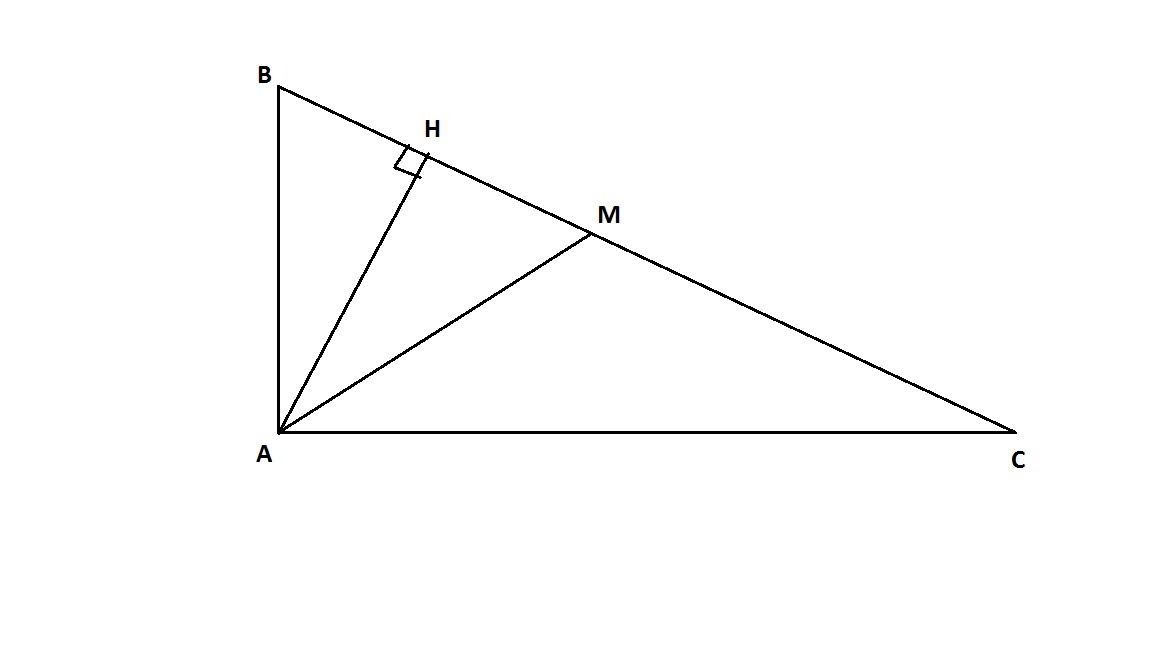
В прямоугольном треугольнике медиана проведенная к гипотенузе равна 50 см, а высота 48 см. Найдите периметр треугольника
Ответы
Автор ответа:
0
Медиана в прямоугольном треугольнике, проведённая к гипотенузе, равна половине гипотенузе.
Тогда
Высота в прямоугольном треугольнике является средним геометрический для проекций катетов на гипотенузу, т.е.:
 .
.
Пусть BH = x. Тогда HC = (100 - x). Получим уравнение:

Значит, BH = 64 или 36, а HC = 36 или 64.
Для удобства пусть BH = 36, а HC = 64.
По теореме Пифагора в ΔABH:

По теореме Пифагора в ΔABC:


Ответ:
Тогда
Высота в прямоугольном треугольнике является средним геометрический для проекций катетов на гипотенузу, т.е.:
Пусть BH = x. Тогда HC = (100 - x). Получим уравнение:
Значит, BH = 64 или 36, а HC = 36 или 64.
Для удобства пусть BH = 36, а HC = 64.
По теореме Пифагора в ΔABH:
По теореме Пифагора в ΔABC:
Ответ:
Приложения:

Похожие вопросы
Предмет: География,
автор: nuzanina9
Предмет: Английский язык,
автор: ibragimovaesma32
Предмет: Алгебра,
автор: 1516805
Предмет: Обществознание,
автор: ficsik3
Предмет: Биология,
автор: kari77