Предмет: Геометрия,
автор: Adilet777
Докажите, что трапеция является равнобедренной тогда и только тогда, когда ее средние линии взаимно перпендикулярны.
Ответы
Автор ответа:
0
Доказательство во вложении
__________________________
__________________________
Приложения:

Автор ответа:
0
Не Адилент, а Адилет, пиши правильно. Пзпхаахахах, да ты что, я только вчера узнал про интернет и как надумал подключить интернет, мде, офф)
Автор ответа:
0
Мда, словарный запас закончился, уважаемый?) Ты если честно надоел, да и ладно мне не лень с тобой переписываться) Евреюшка, я не знаю Украинский язык и не обязан, запомни. А теперь убери палец с карты)
Автор ответа:
0
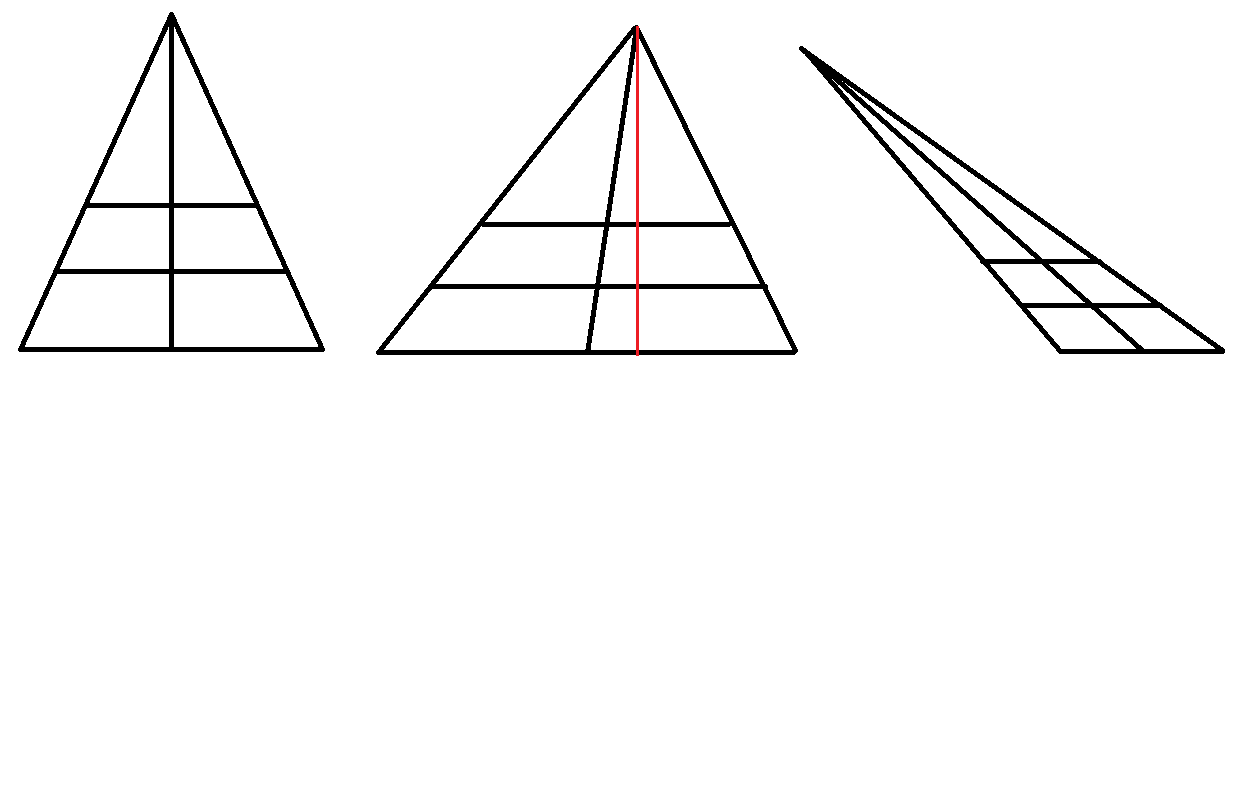
Рассмотрим трапецию, являющуюся равнобочной на рисунке слева, достроим ее до равнобедренного треугольника, средняя линия соединяющая соседние стороны параллельна основаниям трапеции, проведем высоту в равнобедренном треугольнике, как известно, высота в равнобедренном треугольнике является медианой, значит она поделит оба основания на две равные части, и будет являться средней линией соединяющей основания, исходя из свойств высоты равнобедренного треугольника, получаем что эти средние линии взаимо-перпендикулярны.
Теперь рассмотрим произвольную трапецию, на рисунке справа нарисованы возможные варианты произвольных трапеций, аналогично проводим средние линии, в случае когда у треугольника тупой угол, явно видно что является прямым доказательством утверждения, но рассмотрим треугольник с острыми углами, докажем что медиана не перпендикулярна средней линии трапеции:
Так как треугольник произвольный остроугольный, то медиана проведенная из вершины не совпадает с высотой, проведенной на рисунке, тогда получаем что только высота перпендикулярна средней линии трапеции, в то время как медиана делит ее в некотором отношении, в результате получаем что средняя линия соединяющая основания трапеции не перпендикулярна средней линии трапеции(так как не совпадает с высотой) что и требовалось доказать!
Теперь рассмотрим произвольную трапецию, на рисунке справа нарисованы возможные варианты произвольных трапеций, аналогично проводим средние линии, в случае когда у треугольника тупой угол, явно видно что является прямым доказательством утверждения, но рассмотрим треугольник с острыми углами, докажем что медиана не перпендикулярна средней линии трапеции:
Так как треугольник произвольный остроугольный, то медиана проведенная из вершины не совпадает с высотой, проведенной на рисунке, тогда получаем что только высота перпендикулярна средней линии трапеции, в то время как медиана делит ее в некотором отношении, в результате получаем что средняя линия соединяющая основания трапеции не перпендикулярна средней линии трапеции(так как не совпадает с высотой) что и требовалось доказать!
Приложения:
Автор ответа:
0
не понимаю, чего это решение носит статус лучшего, я бы скорее отметил как плагиат: все тоже самое, что и у EpicArctic, только другими словами, да и в оформлении оно проигрывает
Автор ответа:
0
Я бы сказал что ее решение было скопировано с какого то сайта
Автор ответа:
0
Это запрещено правилами сайта
Автор ответа:
0
PhysM я его сделал сам, заметьте сам, а не сама, будьте добры, прежде чем о ком-то писать зайдите в профиль и посмотрите его личные данные
Похожие вопросы
Предмет: Математика,
автор: maxtresh814
Предмет: Химия,
автор: bangtan11
Предмет: Алгебра,
автор: lesyyya5789
Предмет: Алгебра,
автор: royalaqayev1997
Предмет: Математика,
автор: alex1371