Question

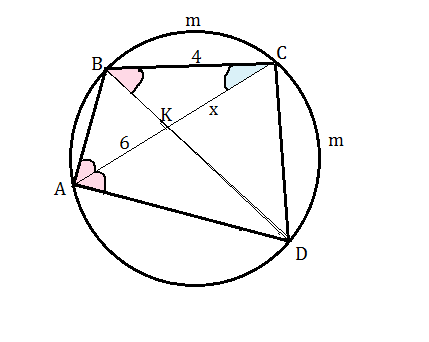
Задача 1. Выпуклый четырехугольник ABCD вписан в окружность. Диагональ AC является биссектрисой угла BAD и пересекается с диаго- налью BD в точке K. Найти длину отрезка KC, если BC = 4, AK = 6.

Answer 1

В решении используем свойства вписанных углов и подобных треугольников. 
АС - биссектриса. 
Равные углы ВАС и САD опираются на равные дуги ВmС и  СmD 
Но на дугу СmD опирается и угол DВС, следовательно, он равен углу ВАС. 
В треугольниках АВС и ВКС имеется общий угол ВСА и равные углы СВК и ВАС Следовательно, они подобны по двум углам. 
Из подобия следует
 АС:ВС=ВС:КС 
ВС²=АС*КС 
16=(6+х)*х 
х²+6х-16=0 
Решив квадратное уравнение, получим два корня: 2 и -8.
Отрицательный корень не подходит. 
Следовательно, КС=х=2