Question

друзья!нужна Ваша помощь.помогите решить задачку по геометрии.
В прямоугольном треугольнике АВС из острых углов проведены медианы, длины которых равны корень из 52 и корень из 73. Определить косинус большего из острых углов.
заранее спасибо!

Answer 1

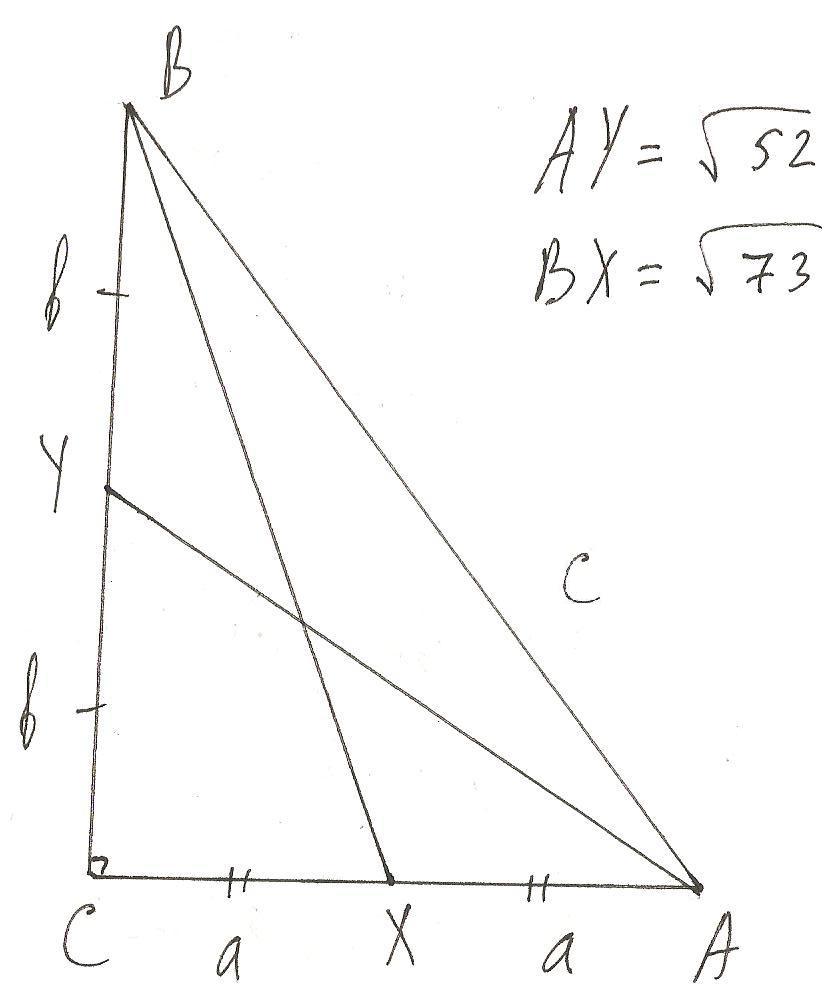
При проведении медиан кроме всего прочего у нас образовалось два прямоугольных треугольника BXC и АУС. Так как АХ и ВУ - медианы, то обозначим ВУ=СУ=b, АХ=СХ=а и запишем теорему Пифагора для указанных выше треугольников:
$left { {{(2a)^2+b^2=( sqrt{52} )^2} atop {a^2+(2b)^2=( sqrt{73} )^2}} right.$
Решим эту систему:
$left { {{4a^2+b^2=52} atop {a^2+4b^2=73}} right. \ b^2=52-4a^2 \ a^2+4(52-4a^2)=73 \ a^2+208-16a^2=73 \ -15a^2=-135 \ a^2=9 \ a=3 \ b^2=52-4cdot3^2=16 \ b=4$
Находим гипотенузу исходного треугольника АВС:
$c= sqrt{(2a)^2+(2b)^2} =sqrt{6^2+8^2} =10$
Так как против большей стороны лежит больший угол, а катет ВС (ВС=8) больше катета АС (АС=6), то большим будет угол, лежащий против стороны ВС, то есть угол А.
$cosA= frac{AC}{AB} =frac{2a}{c} =frac{6}{10} =0.6$
Ответ: 0,6

Answer 2

решение верное)я сдала его уже сегодня))

Answer 3

Пусть КОСИНУС угла, из которого выходит медиана m1 = √52; равен x; а косинус другого угла y; и вторая медиана m2 = √73;
Ясно, что a = c*x; b = c*y; (c гипотенуза, a b катеты);
По теореме косинусов
m2^2 = c^2 + (a/2)^2 - 2*c*(a/2)*x;
или 73 = с^2 +a^2/4 - a^2 = c^2 - 3*a^2/4; (использовано a = c*x)
точно так же 52 = c^2 - 3*b^2/4;
если это сложить, получится 125 = 5*с^2/4; c = 10;
Теперь уже легко найти a и b
73 = c^2 - 3*a^2/4; a^2 = 36; a = 6; b = 8; получился "египетский" треугольник.
Косинус его большего острого угла равен 3/5; (а меньшего 4/5)