Предмет: Алгебра,
автор: Машка98
Народ, помогите решить, если можно все подробно расписать, задание во вложении
Приложения:
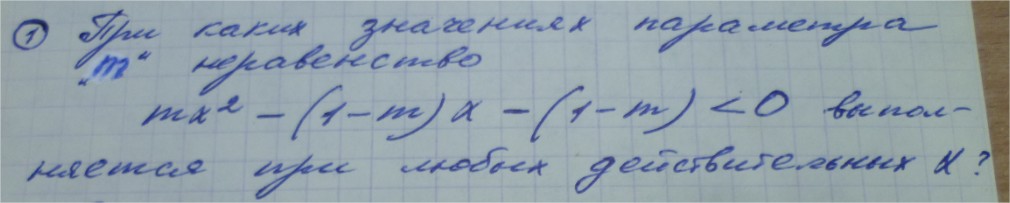
Ответы
Автор ответа:
0
Ответ при m (0;1)
Автор ответа:
0
mx^2-(1-m)x-(1-m)<0
(1-m) не равно 0
-m не равно -1
m не равно1
находим D=0
(1-m)^2-4*m*(-(1-m))=0
(1-m)^2+4*m*(1-m)=0
1-2m+m^2+4m-4m^2=0
-3m^2+2m+1=0
3m^2-2m-1=0
D=(-2)^2-4*3*(-1)=4+12=16=4^2
m1=(-(-2)+4)/2*3=6/6
m1=1-не является решением нашего неравенства
m2=(-(-2)-4)/2*3=-2/6
m2=-1/3-наше решение
mx^2-(1-m)x-(1-m)<0
-1/3x^2-(1-(-1/3))x-(1-(-1/3))<0
-1/3x^2-4/3x-4/3<0-обе части неравенства умножим на (-3)
x^2+4x+4>0
(x+2)^2>0
x+2>0
x>-2
Ответ: при m=-1/3 , x принадлежит (-2;+8],где-(8- бесконечность)
(1-m) не равно 0
-m не равно -1
m не равно1
находим D=0
(1-m)^2-4*m*(-(1-m))=0
(1-m)^2+4*m*(1-m)=0
1-2m+m^2+4m-4m^2=0
-3m^2+2m+1=0
3m^2-2m-1=0
D=(-2)^2-4*3*(-1)=4+12=16=4^2
m1=(-(-2)+4)/2*3=6/6
m1=1-не является решением нашего неравенства
m2=(-(-2)-4)/2*3=-2/6
m2=-1/3-наше решение
mx^2-(1-m)x-(1-m)<0
-1/3x^2-(1-(-1/3))x-(1-(-1/3))<0
-1/3x^2-4/3x-4/3<0-обе части неравенства умножим на (-3)
x^2+4x+4>0
(x+2)^2>0
x+2>0
x>-2
Ответ: при m=-1/3 , x принадлежит (-2;+8],где-(8- бесконечность)
Похожие вопросы
Предмет: Геометрия,
автор: marik566
Предмет: Физика,
автор: donineczhenya
Предмет: Українська мова,
автор: YBeReniy
Предмет: Химия,
автор: Anhtoha983
Предмет: Химия,
автор: Darik97