Предмет: Геометрия,
автор: Mari171
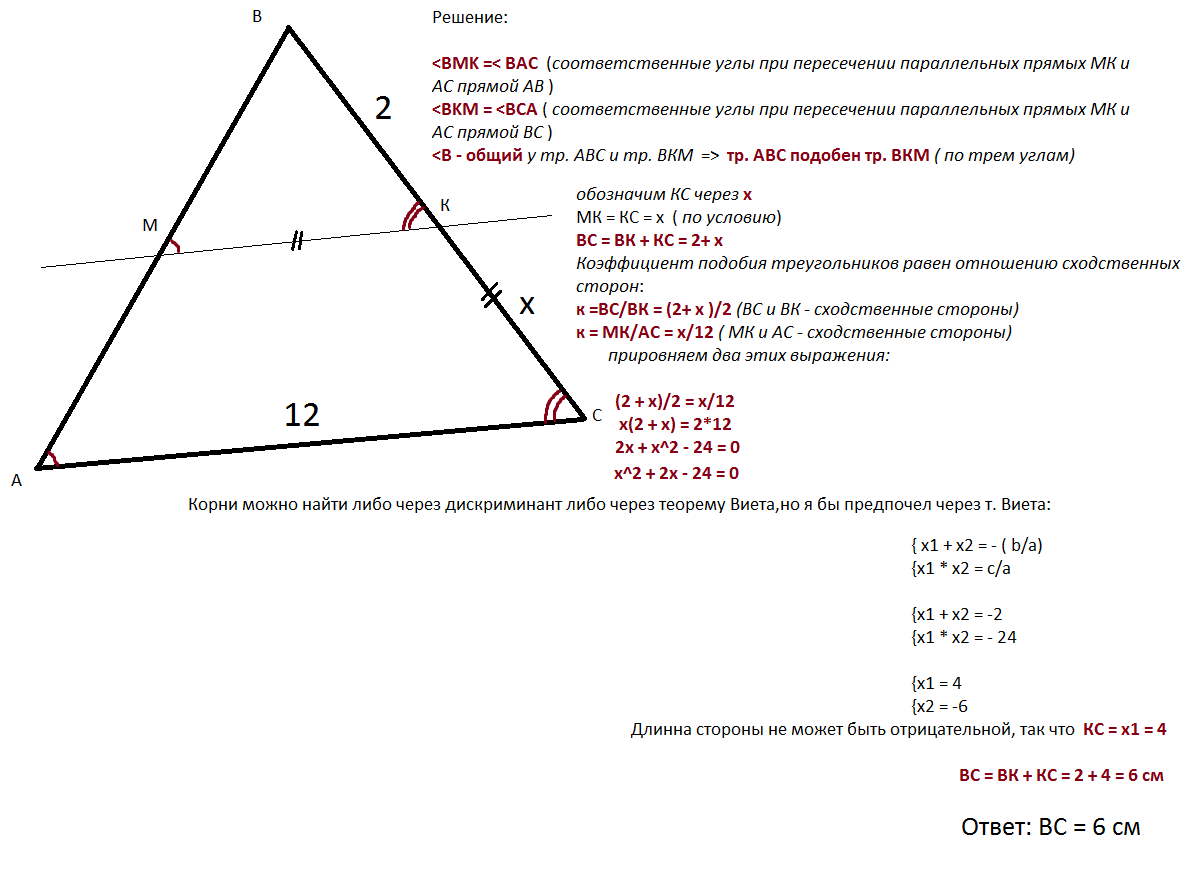
Прямая, параллельная стороне AC треугольника ABC, пересекает его сторону AB в точке M, а сторону BC - в точке K, BK=2 см, AC=12 см, MK=KC. Найдите BC
(напишите, пожалуйсте и свойства или теоремы, которые используете)
Ответы
Автор ответа:
0
Сторона ВС =ВК+КС. Обозначим КС=х. тогда ВС=ВК+х=2+х.
Прямая, параллельная стороне треугольника, отсекает от него подобный треугольник. Поэтому треугольник АВС подобен треугольнику МВК.Значит ,стороны этих треугольников подобны:

По свойству пропорции произведение средних членов равно произведению крайних:

Длина не может быть отрицательной, поэтому х=4.
ВС=2+4=6
Прямая, параллельная стороне треугольника, отсекает от него подобный треугольник. Поэтому треугольник АВС подобен треугольнику МВК.Значит ,стороны этих треугольников подобны:
По свойству пропорции произведение средних членов равно произведению крайних:
Длина не может быть отрицательной, поэтому х=4.
ВС=2+4=6
Автор ответа:
0
Решение во вложении
____________________
____________________
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: 05071978k
Предмет: Алгебра,
автор: OCEANrip
Предмет: Математика,
автор: midinasungatova
Предмет: Алгебра,
автор: zzzrt
Предмет: Алгебра,
автор: DivaRicci