Предмет: Алгебра,
автор: SAHARIA
Решить квадратное уравнение с модулем:
x^2 – |x – 5| = 5
Приложения:
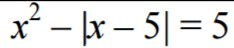
Ответы
Автор ответа:
0
х² -5 = |x-5|
возведем обе части в квадрат, причем х²-5>0
(х²-5)² = (х-5)²
х²-5>0
x²>5 ⇒ |x|>√5
х⁴-10х²+25=х²-10х+25
х⁴-11х²+10х=0
х(x³ -11x +10)=0
x=0 - не подходит
х³ -11х+10=0 - представим этот многочлен в виде множителей
так как х=1 является корнем данного уравнения, то получим
х³ -11х+10=(х-1)(х² +х-10)=0
х=1 - не подходит
х² +х-10=0
D=1+40=41
x₁ = (-1-√41)/2
х₂ = (-1+√41)/2
Ответ: x₁ = (-1-√41)/2
х₂ = (-1+√41)/2
возведем обе части в квадрат, причем х²-5>0
(х²-5)² = (х-5)²
х²-5>0
x²>5 ⇒ |x|>√5
х⁴-10х²+25=х²-10х+25
х⁴-11х²+10х=0
х(x³ -11x +10)=0
x=0 - не подходит
х³ -11х+10=0 - представим этот многочлен в виде множителей
так как х=1 является корнем данного уравнения, то получим
х³ -11х+10=(х-1)(х² +х-10)=0
х=1 - не подходит
х² +х-10=0
D=1+40=41
x₁ = (-1-√41)/2
х₂ = (-1+√41)/2
Ответ: x₁ = (-1-√41)/2
х₂ = (-1+√41)/2
Автор ответа:
0
ОГРОМНОЕ спасибо, очень помогли))))
Похожие вопросы
Предмет: Геометрия,
автор: entoohip
Предмет: Русский язык,
автор: aishaom22
Предмет: Қазақ тiлi,
автор: creepperc
Предмет: Физика,
автор: LeraRosher