Предмет: Алгебра,
автор: PandochkaAlexandra
Ребята!! срочно нужна помощь, помогите решить номера!! Задание - решить тригонометрические выражения и найти корни уравнения в заданном промежутке!! Задания на фото, решите кто-нибудь, сколько сможите, ну хотя бы номеров 5 минимум(((( не понимаю я их вообще, вот буду разбираться с вашей помощью! Спасибо заранее:**
Приложения:
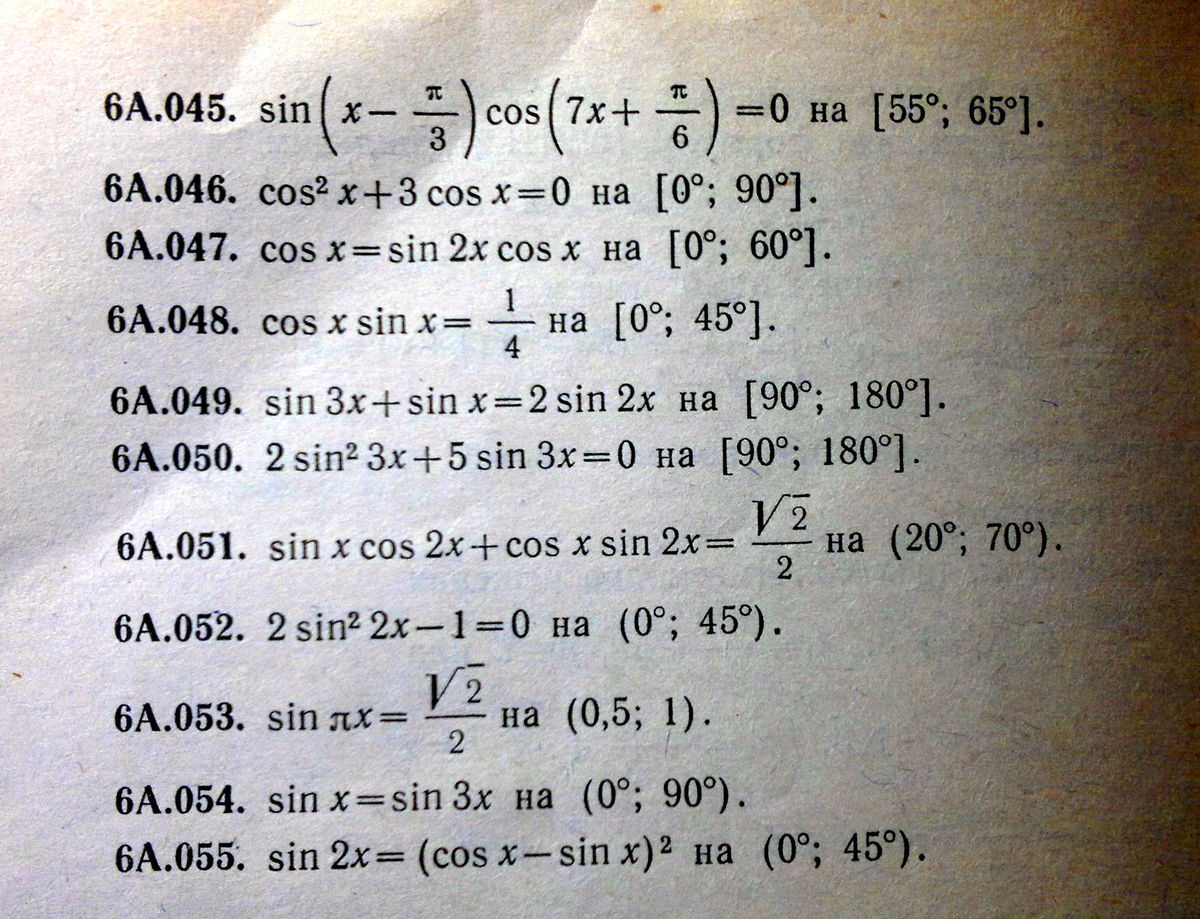
Ответы
Автор ответа:
0
Ответ: х=60 градусов
Ответ: х=90 градусов.
Найденные углы не входят в заданный интервал [0,60].
Ответ:х=45 град.
Ответ: х=15 град.
Ответ: х=15 град.
Похожие вопросы
Предмет: Физика,
автор: Surayyobegaliyeva150
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: obivankenobi23
Предмет: Информатика,
автор: Марат2000
Предмет: Литература,
автор: holli28