Предмет: Алгебра,
автор: ариночкааа
помогите пожалуйста с арифметической прогрессией
Приложения:
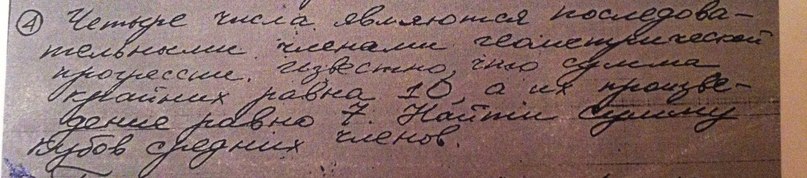
Ответы
Автор ответа:
0
Это условие задачи.Но это и условия теоремы Виета.Поэтому b_1 и b_4 можем найти из квадратного уравнения:
Похожие вопросы
Предмет: Геометрия,
автор: irakondratenko2707
Предмет: Физика,
автор: voitsenkopavlo
Предмет: Английский язык,
автор: mobilochka2019
Предмет: Геометрия,
автор: kapysha