Предмет: Алгебра,
автор: овен6
ТРИГОНОМЕТРИЯ
помогите пожалуйста
Приложения:
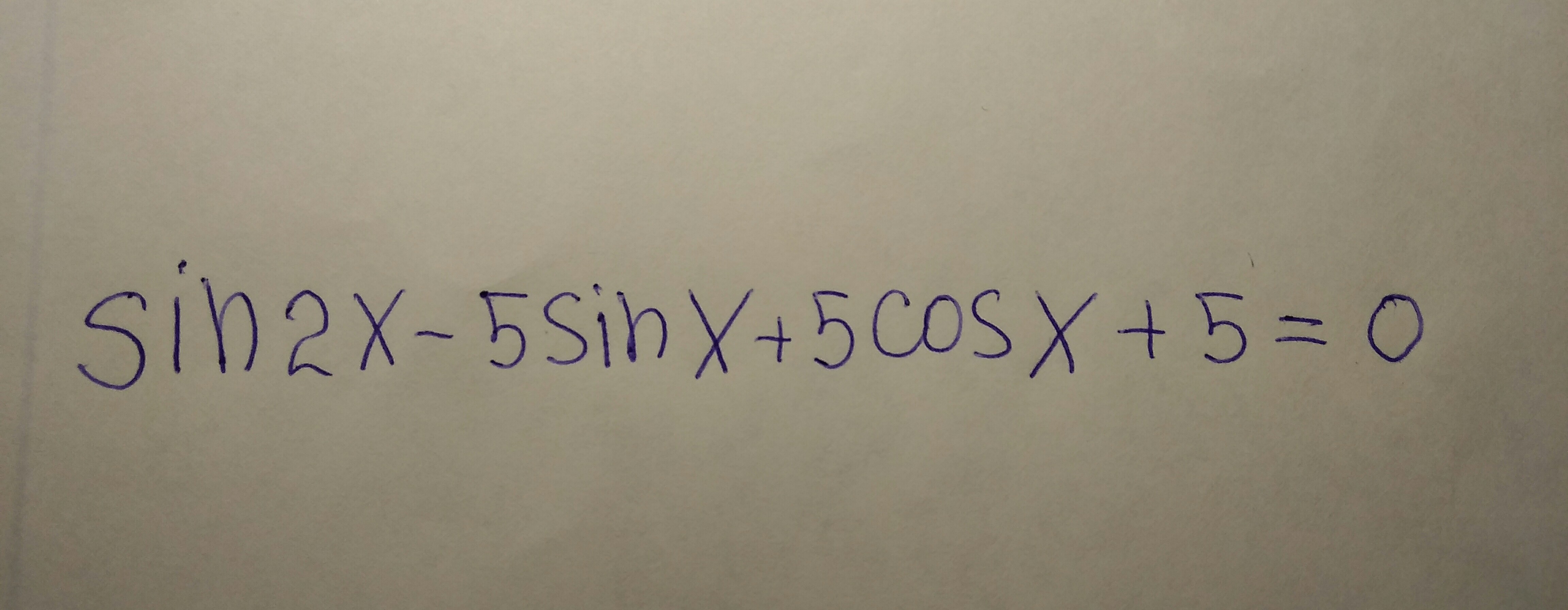
Ответы
Автор ответа:
0
Пусть
Имеем
По т. Виета:
Обратная замена
Вспомним формулы, содержащие дополнительный угол
Ответ:
Автор ответа:
0
у вас неправильно
Похожие вопросы
Предмет: Математика,
автор: saidahrorovhayrullo
Предмет: Алгебра,
автор: Y0ungS
Предмет: Русский язык,
автор: annavinokurova04
Предмет: Математика,
автор: мопрор
Предмет: Алгебра,
автор: Rocton