Question

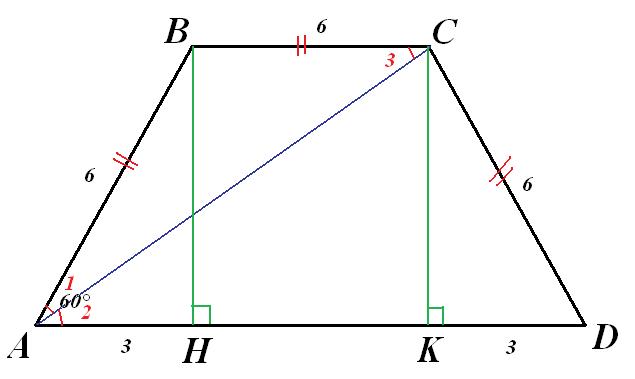
В равнобедренной трапеции ABCD диагональ AC делит угол при нижнем основании AD, равный 60°, пополам. BH − высота трапеции. Найдите Sтрапеции , если меньшее основание равно 6 см.

Answer 1

Чертеж во вложении.
1) Т.к. диагональ АС - биссектриса ∠А, то ∠1=∠2.
Т.к. АД||ВС и АС - секущая , то ∠2=∠3 (накрест лежащие).
Значит, ∠1=∠2=∠3. Поэтому ∆АВС - равнобедренный с основанием АС. Значит, АВ=ВС. Таким образом, АВ=ВС=СД=6см.
2) Опустим высоты ВН и СК. ∆АВН=∆ДСК. Значит, АН=ДК.
В ∆АВН 
$AH=AB*cos angle A=6*cos60^o=6*frac{1}{2}=3=KD\ AD=AH+HK+KD=3+6+3=12\ BH=AB*sin angle A=6*sin60^o=6*frac{sqrt3}{2}=3sqrt3\ S_{ABCD}=frac{AD+BC}{2}*BH=frac{12+6}{2}*3sqrt3=27sqrt3$
Ответ: $27sqrt3$ cм^2